Giải Toán 12 trang 50 tập 1 Kết nối tri thức
Giải Toán 12 trang 50 Tập 1
Giải Toán 12 trang 50 Tập 1 Kết nối tri thức hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 12 Kết nối tri thức tập 1 trang 50.
Luyện tập 3 trang 50 SGK Toán 12 tập 1 Kết nối
Trong Ví dụ 3, hãy tính độ dài của vectơ 
\(\overrightarrow{AC} +\overrightarrow{C'D'}\)
Cho hình lập phương ABCD.A'B'C'D' có độ dài mỗi cạnh bằng 1 (H.2.12).
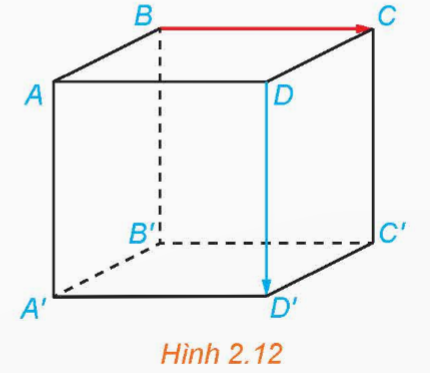
Hướng dẫn giải:
Tứ giác CDD'C' là hình vuông nên \(\overrightarrow{CD} =\overrightarrow{C'D'}\)
Do đó \(\overrightarrow{AC} +\overrightarrow{C'D'} =\overrightarrow{AC} +\overrightarrow{CD}=\overrightarrow{AD}\)
Do hình lập phương có cạnh bằng 1 nên AD = 1.
Suy ra \(|\overrightarrow{AC} +\overrightarrow{C'D'} |=1\)
Luyện tập 4 trang 50 SGK Toán 12 tập 1 Kết nối
Cho tứ diện ABCD (H.2.13). Chứng minh rằng \(\overrightarrow{AB} +\overrightarrow{CD} =\overrightarrow{AD} +\overrightarrow{CB}\).
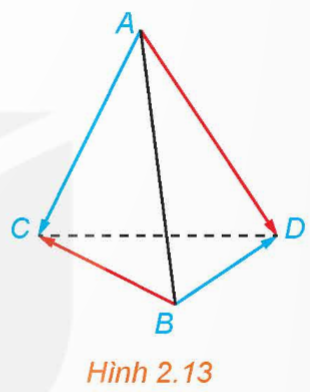
Hướng dẫn giải:
Áp dụng tính chất của phép cộng vectơ trong không gian, ta được:
\(\overrightarrow{AB} +\overrightarrow{CD} =(\overrightarrow{AD} +\overrightarrow{DB} ) + \overrightarrow{CD}\)
\(=\overrightarrow{AD} +(\overrightarrow{DB} + \overrightarrow{CD} )\)
\(=\overrightarrow{AD} +( \overrightarrow{CD} + \overrightarrow{DB})\)
\(=\overrightarrow{AD} + \overrightarrow{CB}\)
Hoạt động 4 trang 50 SGK Toán 12 tập 1 Kết nối
Cho hình hộp ABCD.A'B'C'D' (H.2.14).
a) Hai vectơ \(\overrightarrow{AB} +\overrightarrow{AD}\) và \(\overrightarrow{AC}\) có bằng nhau hay không?
b) Hai vectơ \(\overrightarrow{AB} + \overrightarrow{AD}+\overrightarrow{AA'}\) và \(\overrightarrow{AC'}\) có bằng nhau hay không?
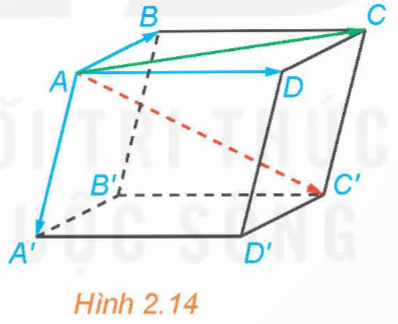
Hướng dẫn giải:
a) Tứ giác ABCD là hình bình hành nên \(\overrightarrow{AB} =\overrightarrow{DC}\)
Do đó \(\overrightarrow{AB} +\overrightarrow{AD} =\overrightarrow{DC} +\overrightarrow{AD}\)
\(= \overrightarrow{AD}+ \overrightarrow{DC} = \overrightarrow{AC}\)
Vậy \(\overrightarrow{AB} +\overrightarrow{AD} =\overrightarrow{AC}\)
b) Tứ giác ACC'A' là hình bình hành nên \(\overrightarrow{AA'} =\overrightarrow{CC'}\)
Do đó \(\overrightarrow{AB} + \overrightarrow{AD}+\overrightarrow{AA'} =(\overrightarrow{AB} + \overrightarrow{AD})+\overrightarrow{AA'}\)
\(=\overrightarrow{AC}+\overrightarrow{CC'}\)
\(=\overrightarrow{AC'}\)
Vậy \(\overrightarrow{AB} + \overrightarrow{AD}+\overrightarrow{AA'} =\overrightarrow{AC'}\)
Luyện tập 5 trang 50 SGK Toán 12 tập 1 Kết nối
Cho hình hộp chữ nhật ABCD.A'B'C'D'. Chứng minh \(\overrightarrow{BB'} +\overrightarrow{CD} +\overrightarrow{AD} =\overrightarrow{BD'}\)
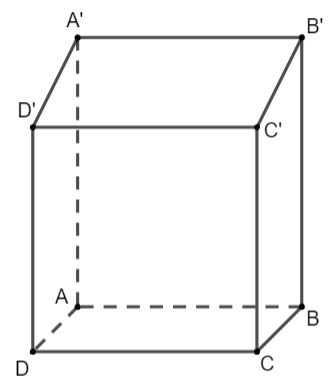
Hướng dẫn giải:
Vì tứ giác ABCD là hình bình hành nên \(\overrightarrow{CD} =\overrightarrow{BA}\) và \(\overrightarrow{AD} =\overrightarrow{BC}\)
Áp dụng quy tắc hình hộp, suy ra:
\(\overrightarrow{BB'} +\overrightarrow{CD} +\overrightarrow{AD} =\overrightarrow{BB'} +\overrightarrow{BA} +\overrightarrow{BC} =\overrightarrow{BD'}\)
-----------------------------------------------
---> Bài tiếp theo: Giải Toán 12 trang 51 tập 1 Kết nối tri thức
Lời giải Toán 12 trang 50 Tập 1 Kết nối tri thức với các câu hỏi nằm trong Bài 6: Vectơ trong không gian, được VnDoc biên soạn và đăng tải!
