Giải Toán 12 trang 15 tập 1 Cánh diều
Giải Toán 12 trang 15 Cánh diều Tập 1
Giải Toán 12 trang 15 Tập 1 hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 12 Cánh diều tập 1 trang 15.
Câu hỏi khởi động trang 15 SGK Toán 12 tập 1
Cho một tấm nhôm có dạng hình vuông cạnh 6 dm. Bác Ánh cắt ở bốn góc bốn hình vuông có cùng độ dài cạnh bằng x (dm), rồi gập tấm nhôm lại như Hình 7 để được một cái hộp có dạng hình hộp chữ nhật không có nắp. Gọi V là thể tích của khối hộp đó.
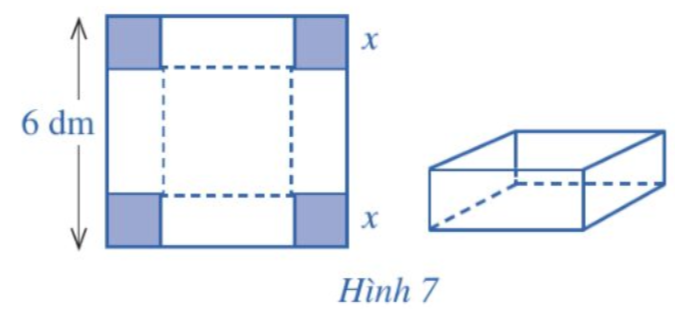
V được tính theo x bởi công thức nào? Có thể tìm giá trị lớn nhất của V bằng cách nào?
Hướng dẫn giải:
Cạnh đáy của khối hộp là: 6 - 2x (dm) (0 < x < 3)
Thể tích của khối hộp là: V(x) = x(6 - 2x)2 (dm3)
Ta có: V'(x) = 12x2 - 48x + 36
V'(x) = 0 ⇔ x = 1 hoặc x = 3
Lập bảng biến thiên của hàm số y = V(x):
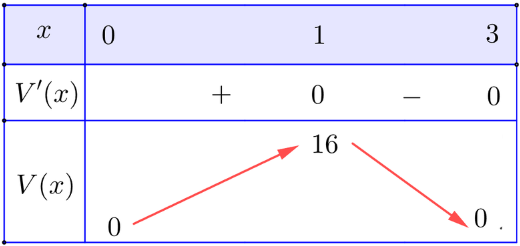
Từ bảng biến thiên, hàm số y = V(x) đạt cực đại tại x = 1.
Hoạt động 1 trang 15 SGK Toán 12 tập 1
Cho hàm số y = f(x) liên tục trên đoạn [– 1; 1] và có đồ thị là đường cong ở Hình 8.
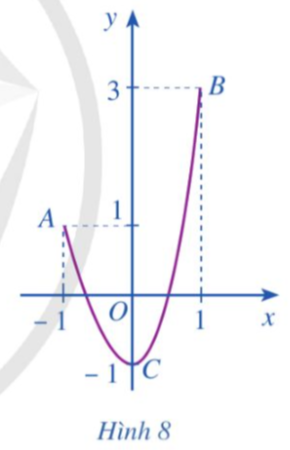
Quan sát đồ thị và cho biết:
a) Điểm nào thuộc đồ thị hàm số có tung độ lớn nhất;
b) Điểm nào thuộc đồ thị hàm số có tung độ nhỏ nhất.
Hướng dẫn giải:
-----------------------------------------------
---> Xem thêm: Giải Toán 12 trang 16 tập 1 Cánh diều
Lời giải Toán 12 trang 15 Tập 1 Cánh diều với các câu hỏi nằm trong Bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số, được VnDoc biên soạn và đăng tải!








