Giải Toán 12 trang 89 tập 1 Cánh diều
Giải Toán 12 trang 89 Cánh diều Tập 1
Giải Toán 12 trang 89 Tập 1 hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 12 Cánh diều tập 1 trang 89.
Hoạt động trang 89 SGK Toán 12 tập 1
Xét mẫu số liệu ghép nhóm cho bởi Bảng 13.
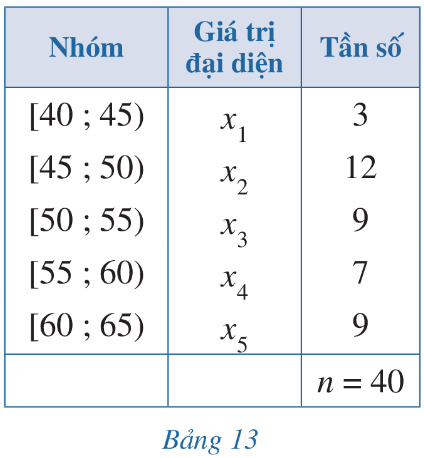
a) Tìm x1; x2; x3; x4; x5 lần lượt là giá trị đại diện của nhóm 1, nhóm 2, nhóm 3, nhóm 4, nhóm 5
b) Tính số trung bình cộng \(\overline x\) của mẫu số liệu ghép nhóm đó
c) Tính \({s^2} = \frac{{3.{{({x_1} - \overline x )}^2} + 12{{({x_2} - \overline x )}^2} + 9{{({x_3} - \overline x )}^2} + 7{{({x_4} - \overline x )}^2} + 9{{({x_5} - \overline x )}^2}}}{{40}}\)
d) Tính \(s = \sqrt {{s^2}}\)
Hướng dẫn giải:
a)
| Nhóm | Giá trị đại diện | Tần số |
[40; 45) [45; 50) [50; 55) [55; 60) [60; 65) | 42,5 47,5 52,5 57,5 62,5 | 3 12 9 7 9 |
n = 40 |
b) Số trung bình của mẫu số liệu ghép nhóm là:
\(\overline{x} =\frac{3.42,5+12.47,5+9.52,5+7.57,5+9.62,5}{40} =53,375\)
c) \(s^2=\frac{1}{40}\left[3.\left(42,5-53,375\right)^2+12.\left(47,5-53,375\right)^2+9.\left(52,5-53,375\right)^2\right]\) \(+\frac{1}{40}\left[7.\left(57,5-53,375\right)^2+9.\left(62,5-53,375\right)^2\right]\approx41,11\)
d) \(s=\sqrt{s^2}\approx\sqrt{41,11}\approx6,41\)
-----------------------------------------------
---> Xem thêm: Giải Toán 12 trang 91 tập 1 Cánh diều
Lời giải Toán 12 trang 89 Tập 1 Cánh diều với các câu hỏi nằm trong Toán 12 Cánh diều Bài 2: Phương sai, độ lệch chuẩn của mẫu số liệu ghép nhóm, được VnDoc biên soạn và đăng tải!
