Giải Toán 12 trang 43 tập 1 Chân trời sáng tạo
Giải Toán 12 trang 43 Tập 1
Giải Toán 12 trang 43 Tập 1 hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 12 Chân trời sáng tạo tập 1 trang 43.
Vận dụng 1 trang 43 SGK Toán 12 tập 1 Chân trời
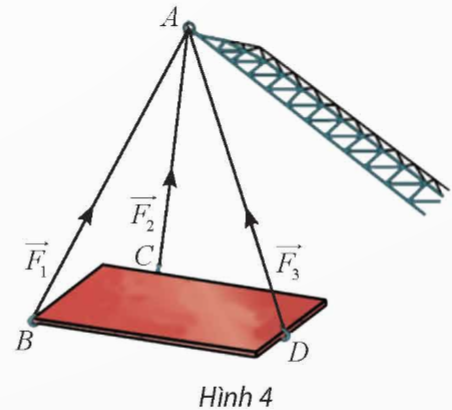
Trong Hình 4, cho biết ba vectơ 
\(\overrightarrow{F_1},\overrightarrow{F_2},\overrightarrow{F_3}\) biểu diễn lực căng của các sợi dây cáp AB, AC, AD tác dụng lên vật nặng. Giá của ba vectơ này có cùng nằm trên một mặt phẳng không?
Hướng dẫn giải:
Do AB, AC, AD là các cạnh bên của một hình chóp tam giác nên giá của ba vectơ đó không cùng nằm trên một mặt phẳng.
Hoạt động 2 trang 43 SGK Toán 12 tập 1 Chân trời
Cho hình hộp ABCD.A'B'C'D' (Hình 5).
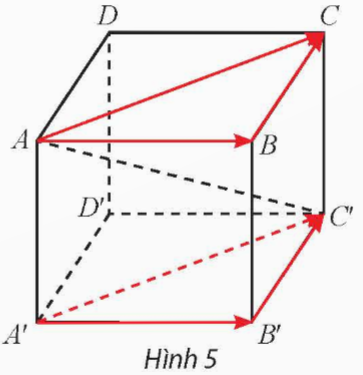
a) Trong mặt phẳng (ABCD), tìm vectơ tổng \(\overrightarrow{AB}+\overrightarrow{BC}\).
Trong mặt phẳng (A'B'C'D'), tìm vectơ tổng \(\overrightarrow{A'B'} + \overrightarrow{B'C'}\).
b) Tìm mối liên hệ giữa các cặp vectơ \(\overrightarrow{AB}\) và \(\overrightarrow{A'B'}, \overrightarrow{BC}\) và \(\overrightarrow{B'C'}, \overrightarrow{AC}\) và \(\overrightarrow{A'C'}\).
c) Giải thích tại sao \(\overrightarrow{AB}+\overrightarrow{BC}= \overrightarrow{A'B'}+\overrightarrow{B'C'}\).
Hướng dẫn giải:
a) Trong mặt phẳng (ABCD), \(\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}\)
Trong mặt phẳng (A'B'C'D'), \(\overrightarrow{A'B'}+\overrightarrow{B'C'}=\overrightarrow{A'C'}\)
b) Trong mp (ABB'A'): \(\overrightarrow{AB}=\overrightarrow{A'B'}\)
Trong mp (BCC'B'): \(\overrightarrow{BC}=\overrightarrow{B'C'}\)
Trong mp (ACC'A'): \(\overrightarrow{AC}=\overrightarrow{A'C'}\)
c) Ta có:
\(\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}\) (câu a)
\(\overrightarrow{A'B'}+\overrightarrow{B'C'}=\overrightarrow{A'C'}\) (câu a)
\(\overrightarrow{AC}=\overrightarrow{A'C'}\) (câu b)
Vậy \(\overrightarrow{AB}+\overrightarrow{BC}= \overrightarrow{A'B'}+\overrightarrow{B'C'}\)
-----------------------------------------------
---> Xem thêm: Giải Toán 12 trang 44 tập 1 Chân trời sáng tạo
Lời giải Toán 12 trang 43 Tập 1 Chân trời sáng tạo với các câu hỏi nằm trong Bài 1: Vectơ và các phép toán trong không gian, được VnDoc biên soạn và đăng tải!
