Giải Toán 12 trang 49 tập 1 Chân trời sáng tạo
Giải Toán 12 trang 49 Tập 1
Giải Toán 12 trang 49 Tập 1 hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 12 Chân trời sáng tạo tập 1 trang 49.
Thực hành 7 trang 49 SGK Toán 12 tập 1 Chân trời
Cho hình lập phương ABCD.A′B′C′D′. Xác định góc 
\((\overrightarrow {AC} ,\overrightarrow {B'D'} ),(\overrightarrow {A'A} ,\overrightarrow {CB'} )\)
Hướng dẫn giải:
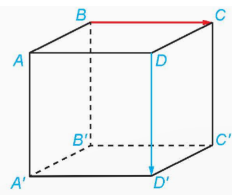
Ta có: \(\overrightarrow{BD}=\overrightarrow{B'D'}\), suy ra \((\overrightarrow{AC},\overrightarrow{B'D'})=(\overrightarrow{AC},\overrightarrow{BD})=90^{\circ}\)
Ta có: \(\overrightarrow{A'A}=\overrightarrow{C'C}\), suy ra \((\overrightarrow{A'A},\overrightarrow{CB'})=(\overrightarrow{C'C},\overrightarrow{CB'})=\widehat{C'CB'}=45^{\circ}\)
Hoạt động 7 trang 49 SGK Toán 12 tập 1 Chân trời
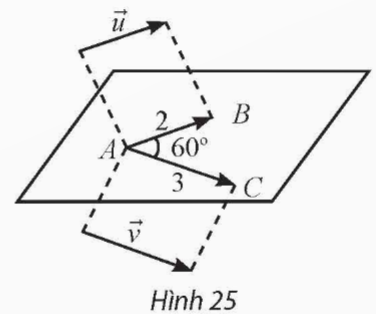
Trong không gian, cho \(\overrightarrow{u\ }\) và \(\overrightarrow{v\ }\) thoả mãn \(\left|\overrightarrow{u\ }\right|=2,\left|\overrightarrow{v\ }\right|=3\). Lấy một điểm A bất kì, gọi B và C là hai điểm sao cho \(\overrightarrow{AB}=\overrightarrow{u},\overrightarrow{AC}=\overrightarrow{v\ }\) (Hình 25). Giả sử \(\widehat {BAC} = 60^\circ\).
a) Tính góc \((\overrightarrow{u},\overrightarrow{v})\)
b) Trong mặt phẳng (ABC), tính tích vô hướng \(\overrightarrow{AB}.\overrightarrow{AC}\)
Hướng dẫn giải:
a) \((\overrightarrow{u},\overrightarrow{v})=(\overrightarrow{AB},\overrightarrow{AC})=60^{\circ}\)
b) Trong mặt phẳng (ABC):
\(\overrightarrow{AB}\cdot\overrightarrow{AC}=|\overrightarrow{AB}|\cdot|\overrightarrow{AC}|\cdot\cos(\overrightarrow{AB},\overrightarrow{AC})\)
-----------------------------------------------
---> Xem thêm: Giải Toán 12 trang 50 tập 1 Chân trời sáng tạo
Lời giải Toán 12 trang 49 Tập 1 Chân trời sáng tạo với các câu hỏi nằm trong Bài 1: Vectơ và các phép toán trong không gian, được VnDoc biên soạn và đăng tải!
