Giải Toán 12 trang 26 tập 1 Kết nối tri thức
Giải Toán 12 trang 26 Tập 1
Giải Toán 12 trang 26 Tập 1 Kết nối tri thức hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 12 Kết nối tri thức tập 1 trang 26.
Mở đầu trang 26 SGK Toán 12 tập 1 Kết nối
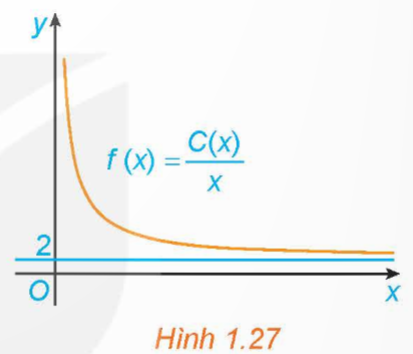
Một đơn vị sản xuất hàng tiêu dùng ước tính chi phí để sản xuất x đơn vị sản phẩm là C(x) = 2x + 45 (triệu đồng). Khi đó chi phí trung bình cho mỗi đơn vị sản phẩm là 
\(f(x) = \frac{C_{(x)} }{x}\). Hãy giải thích tại sao chi phí trung bình giảm theo x nhưng luôn lớn hơn 2 triệu đồng/sản phẩm. Điều này thể hiện trên đồ thị của hàm số f(x) trong Hình 1.27 như thế nào?
Hướng dẫn giải:
Chi phí trung bình cho mỗi đơn vị sản phẩm là: \(f\left(x\right)=\frac{C\left(x\right)}{x}=\frac{2x+45}{x}\)
Ta có: \(\lim_{x\rightarrow +\infty} \frac{2x+45}{x} =2\), nghĩa là x càng tăng thì f(x) càng gần về 2.
Do đó chi phí trung bình giảm theo x nhưng luôn lớn hơn 2 triệu đồng/sản phẩm.
Điều này thể hiện trên đồ thị của hàm số f(x) trong Hình 1.27 là: x → + ∞ thì f(x) → 2, tức là x càng lớn thì chi phí trung bình càng gần về 2 và lớn hơn 2.
Hoạt động 1 trang 26 SGK Toán 12 tập 1 Kết nối
Cho hàm số y = x2 – 4x + 3. Thực hiện lần lượt các yêu cầu sau:
a) Tính y' và tìm các điểm tại đó y' = 0.
b) Xét dấu y' để tìm các khoảng đồng biến, khoảng nghịch biến và cực trị của hàm số.
c) Tính \(\lim_{x\rightarrow -\infty } y, \lim_{x\rightarrow +\infty } y\) và lập bảng biến thiên của hàm số.
d) Vẽ đồ thị của hàm số và nhận xét về tính đối xứng của đồ thị.
Hướng dẫn giải:
Tập xác định của hàm số: R
a) Ta có: y' = 2x – 4; y' = 0 ⇔ x = 2
b) Ta có: y ' > 0 với x ∈ (– ∞; 2); y' < 0 với x ∈ (2; + ∞).
Suy ra hàm số đồng biến trên khoảng (– ∞; 2) và nghịch biến trên khoảng (2; + ∞).
Do đó, hàm số đạt cực tiểu tại x = 2 và yCT = y(2) = – 1. Hàm số không có cực đại.
c) Ta có: \(\lim_{x\rightarrow - \infty} y =\lim_{x\rightarrow - \infty} \left ( x^2-4x+3 \right ) = + \infty\)
\(\lim_{x\rightarrow + \infty} y =\lim_{x\rightarrow + \infty} \left ( x^2-4x+3 \right ) = + \infty\)
Lập bảng biến thiên của hàm số, ta có:
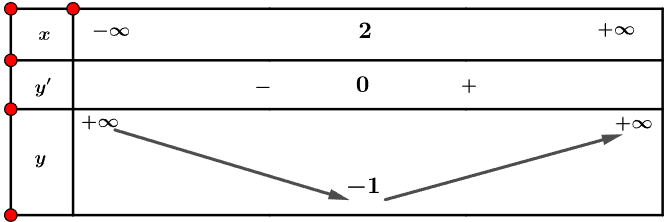
d) Giao điểm của đồ thị hàm số với trục tung là điểm (0; 3).
- Ta có: y = 0 ⇔ x2 – 4x + 3 = 0
⇔ (x – 1)(x – 3) = 0
⇔ x – 1 = 0 hoặc x – 3 = 0
⇔ x = 1 hoặc x = 3.
Do đó, giao điểm của đồ thị hàm số với trục hoành là các điểm (1; 0) và (3; 0).
- Đồ thị hàm số có trục đối xứng là đường thẳng x = 2.
Ta có đồ thị như hình dưới đây:
-----------------------------------------------
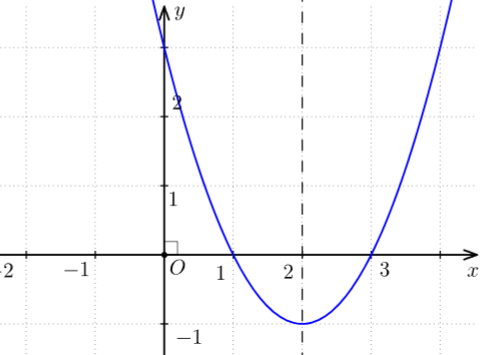
---> Xem thêm: Giải Toán 12 trang 28 tập 1 Kết nối tri thức
Lời giải Toán 12 trang 26 Tập 1 Kết nối tri thức với các câu hỏi nằm trong Bài 4: Khảo sát sự biến thiên và vẽ đồ thị của hàm số, được VnDoc biên soạn và đăng tải!
