Giải Toán 12 trang 56 tập 1 Chân trời sáng tạo
Giải Toán 12 trang 56 Tập 1
Giải Toán 12 trang 56 Tập 1 hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 12 Chân trời sáng tạo tập 1 trang 56.
Thực hành 3 trang 56 SGK Toán 12 tập 1 Chân trời
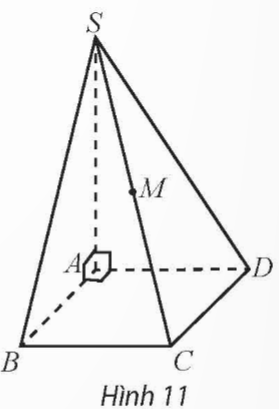
Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng 2, SA vuông góc với mặt phẳng đáy và có độ dài bằng 3 (Hình 11).
a) Vẽ hệ trục toạ độ Oxyz có gốc O trùng với điểm A, các điểm B, D, S lần lượt nằm trên các tia Ox, Oy, Oz và chỉ ra các vectơ đơn vị trên các trục toạ độ.
b) Trong hệ toạ độ nói trên, tìm toạ độ các vectơ 
\(\overrightarrow{AB},\overrightarrow{AD},\overrightarrow{AS}\) và \(\overrightarrow{AM}\) với M là trung điểm của cạnh SC.
Hướng dẫn giải:
a) Các vectơ đon vị lần lượt là: \(\overrightarrow{AB};\ \overrightarrow{AD};\ \overrightarrow{AS}\)
b) \(\overrightarrow{AB}=\left(2;0;0\right);\ \overrightarrow{AD}=\left(0;2;0\right);\ \overrightarrow{AS}=\left(0;0;3\right)\)
\(\overrightarrow{AC}= \overrightarrow{AB}+\overrightarrow{AD}=(2;2;0)\)
Do M là trung điểm của SC, ta có:
\(\overrightarrow{AM}=\frac{1}{2}\left(\overrightarrow{AS}+\overrightarrow{AC}\right)=(1;1;\frac{3}{2})\)
Vận dụng 2 trang 56 SGK Toán 12 tập 1 Chân trời
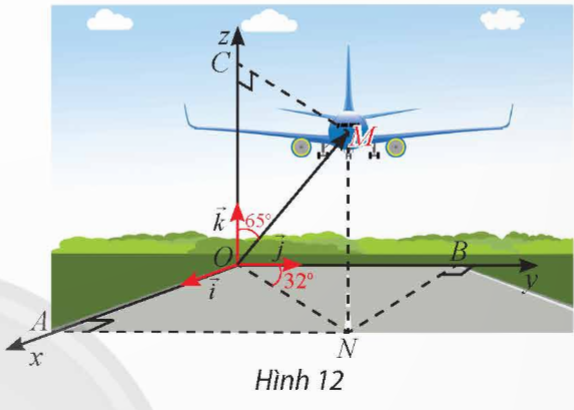
Một máy bay đang cất cánh từ phi trường. Với hệ toạ độ Oxyz được thiết lập như Hình 12, cho biết M là vị trí của máy bay, OM = 14, \(\widehat {NOB} = 32^\circ , \widehat {MOC} = 65^\circ\). Tìm toạ độ điểm M.
Hướng dẫn giải:
Xét tam giác OCM vuông tại C, ta có:
OC = OM . cos \(\widehat {MOC}\)
= 14 . cos 65o ≈ 5,9 cm
CM = ON = OM . sin \(\widehat {MOC}\)
= 14 . sin 65o ≈ 12,7 cm
Xét tam giác OBN vuông tại B, ta có:
OB = ON . cos \(\widehat {NOB}\)
= 12,7 . cos 32o ≈ 10,8 cm
OA = BN = ON . sin \(\widehat {NOB}\)
= 12,7 . sin 32o ≈ 6,7 cm
Do đó A(6,7; 0; 0); B(0; 10,8; 0); C(0; 0; 5,9)
Suy ra M(6,7; 10,8; 5,9).
Bài 1 trang 56 SGK Toán 12 tập 1 Chân trời
Trong không gian Oxyz, biết:
a) \(\overrightarrow{a}=5\overrightarrow{i}+7\overrightarrow{j}-3\overrightarrow{k},\ \overrightarrow{b}=2\overrightarrow{i}+4\overrightarrow{k\ }\). Tìm toạ độ các vectơ \(\overrightarrow{a},\overrightarrow{b\ }\)
b) \(\overrightarrow{OM}=4\overrightarrow{i}-\overrightarrow{j}+3\overrightarrow{k},\ \overrightarrow{ON}=8\overrightarrow{i}-5\overrightarrow{j\ }\). Tìm toạ độ các điểm M, N.
Hướng dẫn giải:
a) Ta có:
\(\overrightarrow{a}=5\overrightarrow{i}+7\overrightarrow{j}-3\overrightarrow{k}\) nên \(\overrightarrow{a}=\left(5;7;-3\right)\)
\(\overrightarrow{b}=2\overrightarrow{i}+4\overrightarrow{k\ }\) nên \(\overrightarrow{b}=\left(2;0;4\right)\)
b) Ta có:
\(\overrightarrow{OM}=4\overrightarrow{i}-\overrightarrow{j}+3\overrightarrow{k\ }\) nên M(4; - 1; 3)
\(\overrightarrow{ON}=8\overrightarrow{i}-5\overrightarrow{j\ \ }\) nên N(8; - 5; 0)
Bài 2 trang 56 SGK Toán 12 tập 1 Chân trời
Trong không gian Oxyz, biết:
a) \(\overrightarrow{a}=(-2;5;-7),\overrightarrow{b}=(4;0;1)\). Tính \(\overrightarrow{a},\overrightarrow{b}\), theo các vectơ \(\overrightarrow{i},\overrightarrow{j},\overrightarrow{k\ }\)
b) A(7; –2; 1), B(0; 5; 0). Tính \(\overrightarrow {OA} , \overrightarrow {OB}\) theo các vectơ \(\overrightarrow{i},\overrightarrow{j},\overrightarrow{k\ }\)
Hướng dẫn giải:
a) Ta có:
\(\overrightarrow{a}=-2\overrightarrow{i}+5\overrightarrow{j}-7\overrightarrow{k\ }\)
\(\overrightarrow{b}=4\overrightarrow{i}+\overrightarrow{k\ }\)
b) \(\overrightarrow{OA}=7\overrightarrow{i}-2\overrightarrow{j}+\overrightarrow{k\ }\)
\(\overrightarrow{OB}=5\overrightarrow{j}\)
Bài 3 trang 56 SGK Toán 12 tập 1 Chân trời
Cho tứ diện SABC có ABC là tam giác vuông tại B, BC = 3, BA = 2, SA vuông góc với mặt phẳng (ABC) và có độ dài bằng 2 (Hình 13).
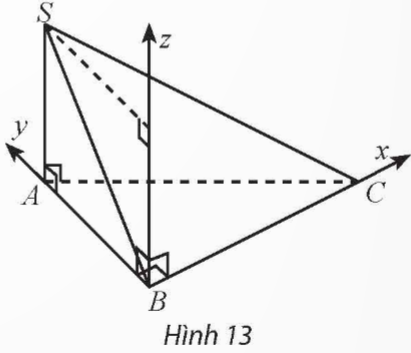
a) Xác định một hệ toạ độ dựa trên gợi ý của hình vẽ và chỉ ra các vectơ đơn vị trên các trục toạ độ.
b) Tìm toạ độ các điểm A, B, C, S.
Hướng dẫn giải:
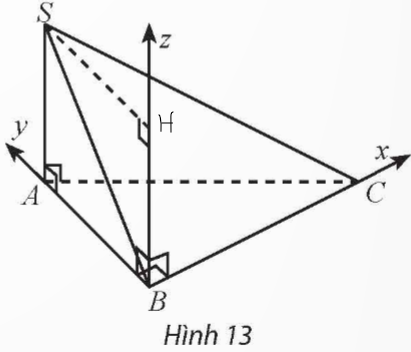
a) Chọn hệ trục tọa độ Oxyz với gốc O trùng với điểm B.
Các vectơ đơn vị trên ba trục Ox, Oy, Oz lần lượt là \(\overrightarrow{BC},\overrightarrow{BA},\overrightarrow{BH\ }\)
b) A(0; 2; 0); B(0; 0; 0); C(3; 0; 0); S(0; 2; 2)
-----------------------------------------------
---> Xem thêm: Giải Toán 12 trang 57 tập 1 Chân trời sáng tạo
Lời giải Toán 12 trang 56 Tập 1 Chân trời sáng tạo với các câu hỏi nằm trong Bài 2: Toạ độ của vectơ trong không gian, được VnDoc biên soạn và đăng tải!
