Giải Toán 12 trang 46 tập 1 Cánh diều

Giải Toán 12 trang 46 Cánh diều Tập 1

Bài 4 trang 46 SGK Toán 12 tập 1
Bài 5 trang 46 SGK Toán 12 tập 1
Bài 6 trang 46 SGK Toán 12 tập 1
Bài 7 trang 46 SGK Toán 12 tập 1

Giải Toán 12 trang 46 Tập 1 hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 12 Cánh diều tập 1 trang 46.

Bài 4 trang 46 SGK Toán 12 tập 1

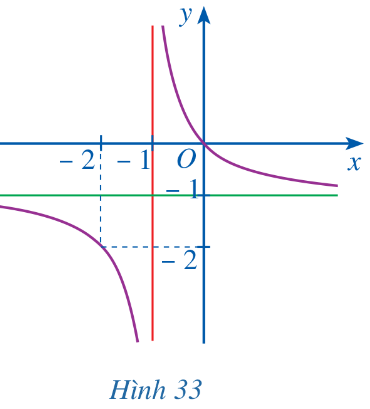
Đường cong ở Hình 33 là đồ thị của hàm số nào sau đây?

A. $y = \frac{x+1}{x-1}$ $y = \frac{x+1}{x-1}$

B. $y = \frac{-x+1}{x+1}$ $y = \frac{-x+1}{x+1}$

C. $y = \frac{x-1}{x+1}$ $y = \frac{x-1}{x+1}$

D. $y = \frac{-x}{x+1}$ $y = \frac{-x}{x+1}$

Hướng dẫn giải:

Đáp án đúng: D

Từ đồ thị ta thấy hàm số có các đường tiệm cận đứng và tiệm cận ngang lần lượt là x = – 1 và y = – 1 => Loại A và C

Vì hàm số đi qua gốc tọa độ nên loại B.

Bài 5 trang 46 SGK Toán 12 tập 1

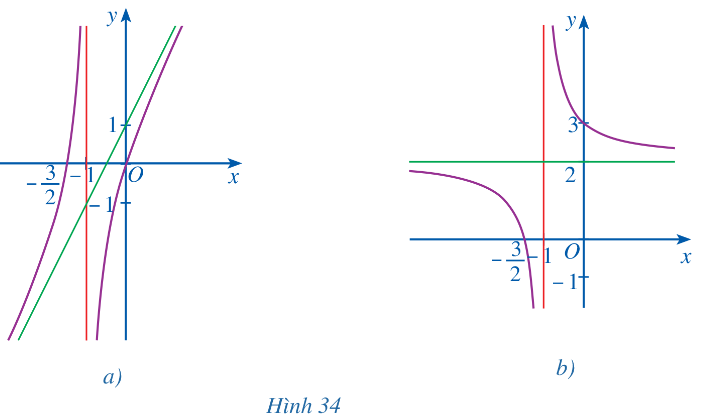
Các đồ thị hàm số ở Hình 34a, Hình 34b đều có đường tiệm cận đứng và đường tiệm cận ngang (hoặc tiệm cận xiên). Hỏi đó là đồ thị của hàm số nào trong các hàm số sau?

a) $y = \frac{2x+3}{x+1}$ $y = \frac{2x+3}{x+1}$

b) $y = \frac{2x-5}{x-1}$ $y = \frac{2x-5}{x-1}$

c) $y = \frac{2x^{2}+3x }{x+1}$ $y = \frac{2x^{2}+3x }{x+1}$

Hướng dẫn giải:

a) Hàm số $y = \frac{2x+3}{x+1}$ $y = \frac{2x+3}{x+1}$ có TCN là đường thẳng y = 2; TCĐ là đường thẳng x = - 1

b) Hàm số $y = \frac{2x-5}{x-1}$ $y = \frac{2x-5}{x-1}$ có TCN là đường thẳng y = 2; TCĐ là đường thẳng x = 1

c) Hàm số $y = \frac{2x^{2}+3x }{x+1}$ $y = \frac{2x^{2}+3x }{x+1}$ có TCĐ là đường thẳng x = - 1; TCX là đường thẳng y = 2x

Vậy: Hình 4a là đồ thị của hàm số $y = \frac{2x^{2}+3x }{x+1}$ $y = \frac{2x^{2}+3x }{x+1}$

Hình 4b là đồ thị của hàm số $y = \frac{2x+3}{x+1}$ $y = \frac{2x+3}{x+1}$

Bài 6 trang 46 SGK Toán 12 tập 1

Tìm các đường tiệm cận ngang và tiệm cận đứng của đồ thị mỗi hàm số sau:

a) $y = \frac{{5x + 1}}{{3x - 2}}$ $y = \frac{{5x + 1}}{{3x - 2}}$

b) $y = \frac{{2{x^3} - 3x}}{{{x^3} + 1}}$ $y = \frac{{2{x^3} - 3x}}{{{x^3} + 1}}$

c) $y = \frac{x}{{\sqrt {{x^2} - 4} }}$ $y = \frac{x}{{\sqrt {{x^2} - 4} }}$

Hướng dẫn giải:

a) $y = \frac{{5x + 1}}{{3x - 2}}$ $y = \frac{{5x + 1}}{{3x - 2}}$

TXĐ của hàm số: $\mathbb {R} \setminus \{ \frac{2}{3} \}$ $\mathbb {R} \setminus \{ \frac{2}{3} \}$

Ta có: $\lim_{x\rightarrow +\infty} f(x) = \lim_{x\rightarrow +\infty} \frac{{5x + 1}}{{3x - 2}} = \frac53$ $\lim_{x\rightarrow +\infty} f(x) = \lim_{x\rightarrow +\infty} \frac{{5x + 1}}{{3x - 2}} = \frac53$

$\lim_{x\rightarrow -\infty} f(x) =\lim_{x\rightarrow -\infty} \frac{{5x + 1}}{{3x - 2}} = \frac53$ $\lim_{x\rightarrow -\infty} f(x) =\lim_{x\rightarrow -\infty} \frac{{5x + 1}}{{3x - 2}} = \frac53$

$\lim_{x\rightarrow \frac23^+} f(x) = \lim_{x\rightarrow \frac23^+} \frac{{5x + 1}}{{3x - 2}} =+\infty$ $\lim_{x\rightarrow \frac23^+} f(x) = \lim_{x\rightarrow \frac23^+} \frac{{5x + 1}}{{3x - 2}} =+\infty$

$\lim_{x\rightarrow \frac23^-} f(x) = \lim_{x\rightarrow \frac23^-} \frac{{5x + 1}}{{3x - 2}} =-\infty$ $\lim_{x\rightarrow \frac23^-} f(x) = \lim_{x\rightarrow \frac23^-} \frac{{5x + 1}}{{3x - 2}} =-\infty$

Vậy $x=\frac{2}{3}$ $x=\frac{2}{3}$ là tiệm cận đứng và y = 3 là tiệm cận ngang của đồ thị hàm số.

b) $y = \frac{{2{x^3} - 3x}}{{{x^3} + 1}} = 2-\frac{{ 3x+2}}{{{x^3} + 1}}$ $y = \frac{{2{x^3} - 3x}}{{{x^3} + 1}} = 2-\frac{{ 3x+2}}{{{x^3} + 1}}$

TXĐ của hàm số: $\mathbb {R} \setminus \{ -1 \}$ $\mathbb {R} \setminus \{ -1 \}$

Ta có: $\lim_{x\rightarrow +\infty} f(x) = \lim_{x\rightarrow +\infty} \frac{{2{x^3} - 3x}}{{{x^3} + 1}} = 2$ $\lim_{x\rightarrow +\infty} f(x) = \lim_{x\rightarrow +\infty} \frac{{2{x^3} - 3x}}{{{x^3} + 1}} = 2$

$\lim_{x\rightarrow -\infty} f(x) =\lim_{x\rightarrow -\infty} \frac{{2{x^3} - 3x}}{{{x^3} + 1}} = 2$ $\lim_{x\rightarrow -\infty} f(x) =\lim_{x\rightarrow -\infty} \frac{{2{x^3} - 3x}}{{{x^3} + 1}} = 2$

Vậy y = 2 là tiệm cận ngang của đồ thị hàm số.

Ta có: $\lim_{x\rightarrow -1^+} f(x) = \lim_{x\rightarrow -1^+} \frac{{2{x^3} - 3x}}{{{x^3} + 1}} =+\infty$ $\lim_{x\rightarrow -1^+} f(x) = \lim_{x\rightarrow -1^+} \frac{{2{x^3} - 3x}}{{{x^3} + 1}} =+\infty$

$\lim_{x\rightarrow -1^-} f(x) = \lim_{x\rightarrow -1^-} \frac{{2{x^3} - 3x}}{{{x^3} + 1}} =-\infty$ $\lim_{x\rightarrow -1^-} f(x) = \lim_{x\rightarrow -1^-} \frac{{2{x^3} - 3x}}{{{x^3} + 1}} =-\infty$

Vậy x = – 1 là tiệm cận đứng của đồ thị hàm số.

c) $y = \frac{x}{{\sqrt {{x^2} - 4} }}$ $y = \frac{x}{{\sqrt {{x^2} - 4} }}$

TXĐ của hàm số: $\mathbb {R} \setminus [-2;2]$ $\mathbb {R} \setminus [-2;2]$

Ta có: $\lim_{x\rightarrow +\infty} f(x) = \lim_{x\rightarrow +\infty} \frac{x}{{\sqrt {{x^2} - 4} }} = 1$ $\lim_{x\rightarrow +\infty} f(x) = \lim_{x\rightarrow +\infty} \frac{x}{{\sqrt {{x^2} - 4} }} = 1$

$\lim_{x\rightarrow -\infty} f(x) = \lim_{x\rightarrow -\infty} \frac{x}{{\sqrt {{x^2} - 4} }} = -1$ $\lim_{x\rightarrow -\infty} f(x) = \lim_{x\rightarrow -\infty} \frac{x}{{\sqrt {{x^2} - 4} }} = -1$

Vậy y = – 1 và y = 1 là tiệm cận ngang của đồ thị hàm số.

Ta có: $\lim_{x\rightarrow -2^-} f(x) = \lim_{x\rightarrow -2^-} \frac{x}{{\sqrt {{x^2} - 4} }} =-\infty$ $\lim_{x\rightarrow -2^-} f(x) = \lim_{x\rightarrow -2^-} \frac{x}{{\sqrt {{x^2} - 4} }} =-\infty$

$\lim_{x\rightarrow 2^+} f(x) = \lim_{x\rightarrow 2^+} \frac{x}{{\sqrt {{x^2} - 4} }} =+\infty$ $\lim_{x\rightarrow 2^+} f(x) = \lim_{x\rightarrow 2^+} \frac{x}{{\sqrt {{x^2} - 4} }} =+\infty$

Vậy x = – 2 và x = 2 là tiệm cận đứng của đồ thị hàm số.

Bài 7 trang 46 SGK Toán 12 tập 1

Tìm các đường tiệm cận đứng và tiệm cận xiên của đồ thị mỗi hàm số sau:

a) $y = x - 3 + \frac{1}{{{x^2}}}$ $y = x - 3 + \frac{1}{{{x^2}}}$

b) $y = \frac{{2{x^2} - 3x + 2}}{{x - 1}}$ $y = \frac{{2{x^2} - 3x + 2}}{{x - 1}}$

c) $y = \frac{{2{x^2} - x + 3}}{{2x + 1}}$ $y = \frac{{2{x^2} - x + 3}}{{2x + 1}}$

Hướng dẫn giải:

a) $y = x - 3 + \frac{1}{{{x^2}}}$ $y = x - 3 + \frac{1}{{{x^2}}}$

TXĐ của hàm số: $\mathbb {R} \setminus \{0\}$ $\mathbb {R} \setminus \{0\}$

Ta có: $\lim_{x\rightarrow 0^+} f(x) = \lim_{x\rightarrow 0^+} \left ( x - 3 + \frac{1}{{{x^2}}} \right ) =+\infty$ $\lim_{x\rightarrow 0^+} f(x) = \lim_{x\rightarrow 0^+} \left ( x - 3 + \frac{1}{{{x^2}}} \right ) =+\infty$

$\lim_{x\rightarrow 0^-} f(x) = \lim_{x\rightarrow 0^-} \left ( x - 3 + \frac{1}{{{x^2}}} \right ) =+\infty$ $\lim_{x\rightarrow 0^-} f(x) = \lim_{x\rightarrow 0^-} \left ( x - 3 + \frac{1}{{{x^2}}} \right ) =+\infty$

Vậy x = 0 là tiệm cận đứng của đồ thị hàm số.

Ta có: $a=\lim_{x\rightarrow +\infty} \frac{f\left( x \right)}{x} =\lim_{x\rightarrow +\infty} \frac{{x - 3 + \frac{1}{{{x^2}}}}}{{x}} =1$ $a=\lim_{x\rightarrow +\infty} \frac{f\left( x \right)}{x} =\lim_{x\rightarrow +\infty} \frac{{x - 3 + \frac{1}{{{x^2}}}}}{{x}} =1$

và $b=\lim_{x\rightarrow +\infty} [f\left( x \right)-x] = \lim_{x\rightarrow +\infty} \left (x - 3 + \frac{1}{{{x^2}}} -x \right ) =-3$ $b=\lim_{x\rightarrow +\infty} [f\left( x \right)-x] = \lim_{x\rightarrow +\infty} \left (x - 3 + \frac{1}{{{x^2}}} -x \right ) =-3$

Tương tự $\lim_{x\rightarrow -\infty} \frac{f\left( x \right)}{x} =1$ $\lim_{x\rightarrow -\infty} \frac{f\left( x \right)}{x} =1$ và $\lim_{x\rightarrow -\infty} [f\left( x \right)-x] =-3$ $\lim_{x\rightarrow -\infty} [f\left( x \right)-x] =-3$

Vậy y = x – 3 là tiệm cận xiên của đồ thị hàm số.

b) $y = \frac{{2{x^2} - 3x + 2}}{{x - 1}} =2x-1-\frac{{1}}{{x - 1}}$ $y = \frac{{2{x^2} - 3x + 2}}{{x - 1}} =2x-1-\frac{{1}}{{x - 1}}$

TXĐ của hàm số: $\mathbb {R} \setminus \{1\}$ $\mathbb {R} \setminus \{1\}$

Ta có: $\lim_{x\rightarrow 1^+} f(x) = \lim_{x\rightarrow 1^+} \left ( 2x-1-\frac{{1}}{{x - 1}} \right ) =-\infty$ $\lim_{x\rightarrow 1^+} f(x) = \lim_{x\rightarrow 1^+} \left ( 2x-1-\frac{{1}}{{x - 1}} \right ) =-\infty$

$\lim_{x\rightarrow 1^-} f(x) = \lim_{x\rightarrow 1^-} \left ( 2x-1-\frac{{1}}{{x - 1}} \right ) =+\infty$ $\lim_{x\rightarrow 1^-} f(x) = \lim_{x\rightarrow 1^-} \left ( 2x-1-\frac{{1}}{{x - 1}} \right ) =+\infty$

Vậy x = 1 là tiệm cận đứng của đồ thị hàm số.

Ta có: $a=\lim_{x\rightarrow +\infty} \frac{f\left( x \right)}{x} =\lim_{x\rightarrow +\infty} \frac{{2x-1-\frac{{1}}{{x - 1}} }}{{x}} =2$ $a=\lim_{x\rightarrow +\infty} \frac{f\left( x \right)}{x} =\lim_{x\rightarrow +\infty} \frac{{2x-1-\frac{{1}}{{x - 1}} }}{{x}} =2$

và $b=\lim_{x\rightarrow +\infty} [f\left( x \right)-2x] = \lim_{x\rightarrow +\infty} \left (2x-1-\frac{{1}}{{x - 1}} -2x \right ) =-1$ $b=\lim_{x\rightarrow +\infty} [f\left( x \right)-2x] = \lim_{x\rightarrow +\infty} \left (2x-1-\frac{{1}}{{x - 1}} -2x \right ) =-1$

Tương tự $\lim_{x\rightarrow -\infty} \frac{f\left( x \right)}{x} =2$ $\lim_{x\rightarrow -\infty} \frac{f\left( x \right)}{x} =2$ và $\lim_{x\rightarrow -\infty} [f\left( x \right)-2x] =-1$ $\lim_{x\rightarrow -\infty} [f\left( x \right)-2x] =-1$

Vậy y = 2x – 1 là tiệm cận xiên của đồ thị hàm số.

c) $y = \frac{{2{x^2} - x + 3}}{{2x + 1}} = x-1+\frac{{4}}{{2x + 1}}$ $y = \frac{{2{x^2} - x + 3}}{{2x + 1}} = x-1+\frac{{4}}{{2x + 1}}$

TXĐ của hàm số: $\mathbb{R}\setminus \{\frac12\}$ $\mathbb{R}\setminus \{\frac12\}$

Ta có: $\lim_{x\rightarrow \frac{1}{2}^+ } f(x) =\lim_{x\rightarrow \frac{1}{2}^+ } \left ( x-1+\frac{{4}}{{2x + 1}} \right )=+\infty$ $\lim_{x\rightarrow \frac{1}{2}^+ } f(x) =\lim_{x\rightarrow \frac{1}{2}^+ } \left ( x-1+\frac{{4}}{{2x + 1}} \right )=+\infty$

$\lim_{x\rightarrow \frac{1}{2}^- } f(x) =\lim_{x\rightarrow \frac{1}{2}^-} \left ( x-1+\frac{{4}}{{2x + 1}} \right )=-\infty$ $\lim_{x\rightarrow \frac{1}{2}^- } f(x) =\lim_{x\rightarrow \frac{1}{2}^-} \left ( x-1+\frac{{4}}{{2x + 1}} \right )=-\infty$

Vậy x = $\frac{1}{2}$ $\frac{1}{2}$ là tiệm cận đứng của đồ thị hàm số.

Ta có: $a=\lim_{x\rightarrow +\infty} \frac{f\left( x \right)}{x} =\lim_{x\rightarrow +\infty} \frac{{x - 1 + \frac{4}{{{2x+1}}}}}{{x}} =1$ $a=\lim_{x\rightarrow +\infty} \frac{f\left( x \right)}{x} =\lim_{x\rightarrow +\infty} \frac{{x - 1 + \frac{4}{{{2x+1}}}}}{{x}} =1$

và $b=\lim_{x\rightarrow +\infty} [f\left( x \right)-x] = \lim_{x\rightarrow +\infty} \left (x - 1 + \frac{4}{{{2x+1}}} -x \right ) =-1$ $b=\lim_{x\rightarrow +\infty} [f\left( x \right)-x] = \lim_{x\rightarrow +\infty} \left (x - 1 + \frac{4}{{{2x+1}}} -x \right ) =-1$

Tương tự $\lim_{x\rightarrow -\infty} \frac{f\left( x \right)}{x} =1$ $\lim_{x\rightarrow -\infty} \frac{f\left( x \right)}{x} =1$ và $\lim_{x\rightarrow -\infty} [f\left( x \right)-x] =-1$ $\lim_{x\rightarrow -\infty} [f\left( x \right)-x] =-1$

Vậy y = x – 1 là tiệm cận xiên của đồ thị hàm số.

-----------------------------------------------

---> Xem thêm: Giải Toán 12 trang 47 tập 1 Cánh diều

Lời giải Toán 12 trang 46 Tập 1 Cánh diều với các câu hỏi nằm trong Bài tập cuối chương 1, được VnDoc biên soạn và đăng tải!

Chia sẻ, đánh giá bài viết

1

74

Bài trước

Bài sau