VnDoc.com

Giải Toán 12 trang 17 tập 1 Kết nối tri thức

Bài trước

Bài sau

Giải Toán 12 trang 17 Tập 1

Luyện tập 1 trang 17 SGK Toán 12 tập 1 Kết nối
Hoạt động 2 trang 17 SGK Toán 12 tập 1 Kết nối

Giải Toán 12 trang 17 Tập 1 Kết nối tri thức hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 12 Kết nối tri thức tập 1 trang 17.

Luyện tập 1 trang 17 SGK Toán 12 tập 1 Kết nối

Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau:

$a) y = \sqrt{2x - x^{2} }$ $a) y = \sqrt{2x - x^{2} }$

$b) y = -x + \frac{1}{x-1}$ $b) y = -x + \frac{1}{x-1}$ trên khoảng (1;+ $\infty$ $\infty$)

Hướng dẫn giải:

a) $y=\sqrt{2x-x^2}$ $y=\sqrt{2x-x^2}$

Tập xác định của hàm số là: [0; 2]

Ta có:

$y=\sqrt{2x-x^2} \ge0$ $y=\sqrt{2x-x^2} \ge0$; dấu bằng xảy ra khi 2x - x² = 0, tức là khi x = 0 hoặc x = 2.

Do đó $\underset{[-1;1]}{min} \ y= y(0) = y(2) = 0$ $\underset{[-1;1]}{min} \ y= y(0) = y(2) = 0$.

$y=\sqrt{2x-x^2} \le0$ $y=\sqrt{2x-x^2} \le0$; dấu bằng xảy ra khi 2x - x² = 1, tức là x = 1.

Do đó $\underset{[-1;1]}{max} \ y= y(1) = 1$ $\underset{[-1;1]}{max} \ y= y(1) = 1$

b) $y=-x+\frac{1}{x-1}$ $y=-x+\frac{1}{x-1}$ trên khoảng (1; +∞)

Với x ∈ (1; +∞), ta có: $y'=-1-\frac{1}{\left(x-1\right)^2} <0$

Tính các giới hạn:

$\lim_{x\rightarrow 1^+} y=\lim_{x\rightarrow 1^+} \left ( -x+\frac{1}{x - 1} \right ) =+ \infty$ $\lim_{x\rightarrow 1^+} y=\lim_{x\rightarrow 1^+} \left ( -x+\frac{1}{x - 1} \right ) =+ \infty$

$\lim_{x\rightarrow +\infty } y=\lim_{x\rightarrow +\infty } \left ( -x+\frac{1}{x - 1} \right ) = - \infty$ $\lim_{x\rightarrow +\infty } y=\lim_{x\rightarrow +\infty } \left ( -x+\frac{1}{x - 1} \right ) = - \infty$

Lập bảng biến thiên của hàm số trên khoảng (1; +∞):

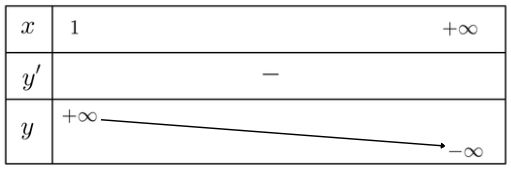
Từ bảng biến thiên, hàm số không có giá trị lớn nhất và giá trị nhỏ nhất.

Hoạt động 2 trang 17 SGK Toán 12 tập 1 Kết nối

Xét hàm số y = f(x) = x³ – 2x² + 1 trên đoạn [−1; 2] với đồ thị như hình 1.16.

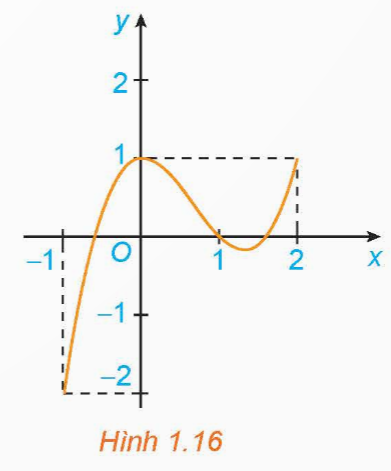
a) Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn [−1; 2].

b) Tính đạo hàm f'(x) và tìm các điểm x ∈ (−1; 2) mà f'(x) = 0.

c) Tính giá trị của hàm số tại hai đầu mút của đoạn [−1; 2] và tại các điểm x đã tìm ở câu b. So sánh số nhỏ nhất trong các giá trị này với $\underset{[-1;2]}{\min} f(x)$ $\underset{[-1;2]}{\min} f(x)$ , số lớn nhất trong các giá trị này với $\underset{[-1;2]}{\max} f(x)$ $\underset{[-1;2]}{\max} f(x)$.

Hướng dẫn giải:

Đang cập nhật....

-----------------------------------------------

---> Xem thêm: Giải Toán 12 trang 18 tập 1 Kết nối tri thức

Lời giải Toán 12 trang 17 Tập 1 Kết nối tri thức với các câu hỏi nằm trong Bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số, được VnDoc biên soạn và đăng tải!

Chia sẻ, đánh giá bài viết

1

118

Bài trước

Bài sau