Giải Toán 12 trang 60 tập 1 Chân trời sáng tạo

Giải Toán 12 trang 60 Tập 1

Thực hành 2 trang 60 SGK Toán 12 tập 1 Chân trời
Vận dụng 2 trang 60 SGK Toán 12 tập 1 Chân trời
Hoạt động 3 trang 60 SGK Toán 12 tập 1 Chân trời

Giải Toán 12 trang 60 Tập 1 hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 12 Chân trời sáng tạo tập 1 trang 60.

Thực hành 2 trang 60 SGK Toán 12 tập 1 Chân trời

Cho ba vectơ $\overrightarrow m = ( - 5;4;9), \overrightarrow n = (2; - 7;0), \overrightarrow p = (6;3; - 4)$ $\vec{m} = (- 5; 4; 9), \vec{n} = (2; - 7; 0), \vec{p} = (6; 3; - 4)$ .

a) Tính $\overrightarrow{m}.\overrightarrow{n},\overrightarrow{m}.\overrightarrow{p\ }$ $\vec{m} . \vec{n}, \vec{m} . \vec{p}$

b) Tính $|\overrightarrow{m}|,|\overrightarrow{n}|,\cos(\overrightarrow{m},\overrightarrow{n})$ $| \vec{m} |, | \vec{n} |, \cos (\vec{m}, \vec{n})$

c) Cho $\overrightarrow{q}=(1;-2;0)$ $\vec{q} = (1; - 2; 0)$ . Vectơ $\overrightarrow{q\ }$ $\vec{q}$ có vuông góc với $\overrightarrow{p\ }$ $\vec{p}$ không?

Hướng dẫn giải:

a) Ta có: $\overrightarrow{m}.\overrightarrow{n\ }$ $\vec{m} . \vec{n}$ = (- 5) . 2 + 4. (- 7) + 9 . 0 = - 38

$\overrightarrow{m}.\overrightarrow{p\ }$ $\vec{m} . \vec{p}$ = (- 5) . 6 + 4 . 3 + 9 . (- 4) = - 54

b) $|\overrightarrow{m}|=\sqrt{\left(-5\right)^2+4^2+9^2}=\sqrt{122}$ $| \vec{m} | = \sqrt{{(- 5)}^{2} + 4^{2} + 9^{2}} = \sqrt{122}$

$|\overrightarrow{n}|=\sqrt{2^2+\left(-7\right)^2+0^2}=\sqrt{53}$ $| \vec{n} | = \sqrt{2^{2} + {(- 7)}^{2} + 0^{2}} = \sqrt{53}$

$\cos(\overrightarrow{m},\overrightarrow{n})=\frac{\overrightarrow{m}.\overrightarrow{n}}{\left|\overrightarrow{m}\right|.\left|\overrightarrow{n}\right|}=\frac{-38}{\sqrt{122}.\sqrt{53}}\approx-0,468$ $\cos (\vec{m}, \vec{n}) = \frac{\vec{m} . \vec{n}}{| \vec{m} | . | \vec{n} |} = \frac{- 38}{\sqrt{122} . \sqrt{53}} \approx - 0, 468$

c) Ta có: $\overrightarrow{q}.\overrightarrow{p\ }$ $\vec{q} . \vec{p}$ = 0

Vậy vectơ $\overrightarrow{q\ }$ $\vec{q}$ có vuông góc với $\overrightarrow{p\ }$ $\vec{p}$

Vận dụng 2 trang 60 SGK Toán 12 tập 1 Chân trời

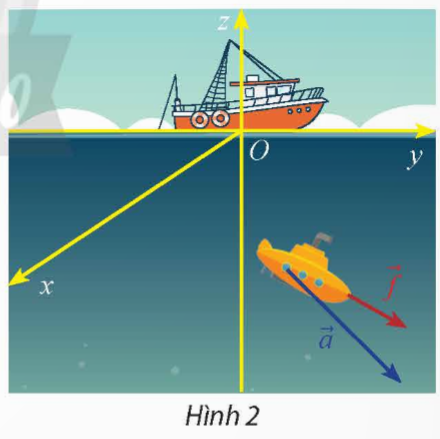
Một thiết bị thăm dò đáy biển (Hình 2) được đẩy bởi một lực $\overrightarrow{f}=(5;4;-2)$ $\vec{f} = (5; 4; - 2)$ (đơn vị: N) giúp thiết bị thực hiện độ dời $\overrightarrow a = (70;20; - 40)$ $\vec{a} = (70; 20; - 40)$ (đơn vị: m). Tính công sinh bởi lực $\overrightarrow{f\ }$ $\vec{f}$

Hướng dẫn giải:

Công sinh bởi lực $\overrightarrow{f\ }$ $\vec{f}$ khi thực hiện độ dời $\overrightarrow{a\ }$ $\vec{a}$ là:

$A=\overrightarrow{f\ }.\overrightarrow{a}=5.70+4.20+\left(-2\right).\left(-40\right)=510$ $A = \vec{f} . \vec{a} = 5.70 + 4.20 + (- 2) . (- 40) = 510$ (N)

Hoạt động 3 trang 60 SGK Toán 12 tập 1 Chân trời

Cho hai điểm $A({x_A};{y_A};{z_A}),B({x_B};{y_B};{z_B})$ $A (x_{A}; y_{A}; z_{A}), B (x_{B}; y_{B}; z_{B})$ . Từ biểu thức $\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}$ $\vec{A B} = \vec{O B} - \vec{O A}$ , tìm toạ độ của vectơ $\overrightarrow{AB}$ $\vec{A B}$ theo toạ độ hai điểm A, B.

Hướng dẫn giải:

$\overrightarrow{OA}=\left(x_A;y_A;z_A\right);\ \overrightarrow{OB}=\left(x_B;y_B;z_B\right)$ $\vec{O A} = (x_{A}; y_{A}; z_{A}); \vec{O B} = (x_{B}; y_{B}; z_{B})$

Vậy $\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}=\left(x_B-x_A;y_B-y_A;z_B-z_A\right)$ $\vec{A B} = \vec{O B} - \vec{O A} = (x_{B} - x_{A}; y_{B} - y_{A}; z_{B} - z_{A})$

-----------------------------------------------

---> Xem thêm: Giải Toán 12 trang 61 tập 1 Chân trời sáng tạo

Lời giải Toán 12 trang 60 Tập 1 Chân trời sáng tạo với các câu hỏi nằm trong Bài 3: Biểu thức toạ độ của các phép toán vectơ, được VnDoc biên soạn và đăng tải!

Xem thêm các bài Tìm bài trong mục này khác:

Chia sẻ, đánh giá bài viết

1

74

Bài trước

Bài sau

Chia sẻ bởi:
Lê Jelar

Đóng Chỉ thành viên VnDoc PRO/PROPLUS tải được nội dung này!

Đóng

79.000 / tháng

Mua ngay

Đặc quyền các gói Thành viên

PRO

Phổ biến nhất

PRO+

Tải tài liệu Cao cấp 1 Lớp

Tải tài liệu Trả phí + Miễn phí

Xem nội dung bài viết

Trải nghiệm Không quảng cáo

Làm bài trắc nghiệm không giới hạn

Tìm hiểu thêm

Mua cả năm Tiết kiệm tới 48%

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!