Giải Toán 12 trang 15 tập 1 Kết nối tri thức
Giải Toán 12 trang 15 Tập 1
Giải Toán 12 trang 15 Tập 1 Kết nối tri thức hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 12 Kết nối tri thức tập 1 trang 15.
Mở đầu trang 15 SGK Toán 12 tập 1 Kết nối
Từ một tấm bìa carton hình vuông có độ dài cạnh bằng 60 cm, người ta cắt bốn hình vuông bằng nhau ở bốn góc rồi gập thành một chiếc hộp có dạng hình hộp chữ nhật không có nắp (H.1.14). Tính cạnh của các hình vuông bị cắt sao cho thể tích của chiếc hộp là lớn nhất.
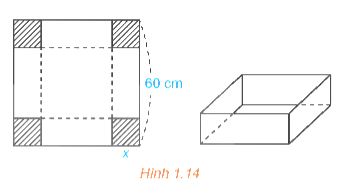
Hướng dẫn giải:
Đang cập nhật...
Hoạt động 1 trang 15 SGK Toán 12 tập 1 Kết nối
Cho hàm số y = f(x) = x2 - 2x với x ∈ [0; 3], có đồ thị như Hình 1.15.
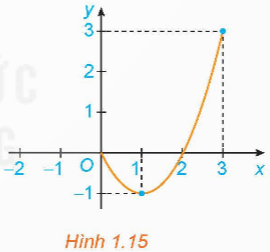
a) Giá trị lớn nhất M của hàm số trên đoạn [0; 3] là bao nhiêu? Tìm x0 sao cho f(x0) = M.
b) Giá trị nhỏ nhất m của hàm số trên đoạn [0; 3] là bao nhiêu? Tìm x0 sao cho f(x0) = m.
Hướng dẫn giải:
a) M = 3
Tại x0 = 3 thì f(x0) = f(3) = M.
b) m = - 1
Tại x0 = 1 thì f(x0) = f(1) = m.
-----------------------------------------------
---> Xem thêm: Giải Toán 12 trang 17 tập 1 Kết nối tri thức
Lời giải Toán 12 trang 15 Tập 1 Kết nối tri thức với các câu hỏi nằm trong Bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số, được VnDoc biên soạn và đăng tải!








