Giải Toán 12 trang 12 tập 1 Kết nối tri thức
Giải Toán 12 trang 12 Tập 1
Giải Toán 12 trang 12 Tập 1 Kết nối tri thức hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 12 Kết nối tri thức tập 1 trang 12.
Luyện tập 5 trang 12 SGK Toán 12 tập 1 KNTT
Tìm cực trị của các hàm số sau:
a) y = x4 - 3x2 + 1
b) 
\(y=\frac{-x^2+2x-1}{x+2}\)
Hướng dẫn giải:
a) y = x4 - 3x2 + 1
Tập xác định của hàm số là R.
Ta có: y' = 4x3 - 6x = 2x(2x2 - 3)
y' = 0 \(\Leftrightarrow\) x = 0 hoặc \(x= -\frac{\sqrt{6} }{2}\) hoặc \(x= \frac{\sqrt{6} }{2}\)
Lập bảng biến thiên của hàm số:
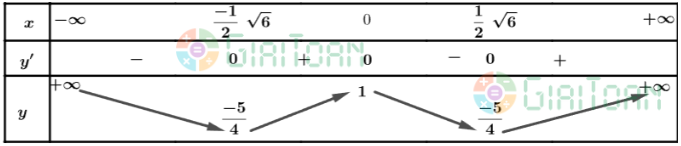
Từ bảng biến thiên, ta có:
Hàm số đạt cực tiểu tại \(x= -\frac{\sqrt{6} }{2}\) và yCT = \(y\left(-\frac{\sqrt{6}}{2}\right)=-\frac{5}{4}\)
Hàm số đạt cực tiểu tại \(x= \frac{\sqrt{6} }{2}\) và yCT = \(y\left(\frac{\sqrt{6}}{2}\right)=-\frac{5}{4}\)
Hàm số đạt cực đại tại x = 0 và yCĐ = y(0) = 1.
b) \(y=\frac{-x^2+2x-1}{x+2}\)
Tập xác định của hàm số là R \ {- 2}
Ta có: \(y'=\frac{\left(-2x+2\right)\left(x+2\right)-\left(-x^2+2x-1\right)}{\left(x+2\right)^2}=\frac{-x^2-4x+5}{\left(x+2\right)^2}\)
y' = 0 \(\Leftrightarrow\) x = 1 hoặc x = - 5.
Lập bảng biến thiên của hàm số:
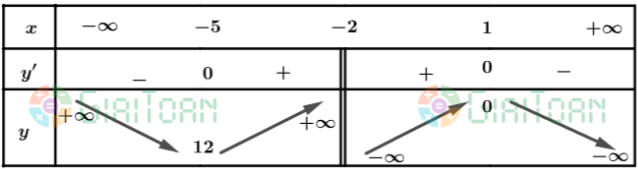
Từ bảng biến thiên, ta có:
Hàm số đạt cực tiểu tại x = - 5 và yCT = y(- 5) = 12
Hàm số đạt cực đại tại x = 1 và yCĐ = y(1) = 0.
Vận dụng 2 trang 12 SGK Toán 12 tập 1 KNTT
Một vật được phóng thẳng đứng lên trên từ độ cao 2m với vận tốc ban đầu là 24,5m/s. Trong Vật lí, ta biết rằng khi bỏ qua sức cản của không khí thì độ cao h (mét) của vật sau t (giây) được cho bởi công thức:
h(t) = 2 + 24,5t - 4,9t2.
Hỏi tại thời điểm nào thì vật đạt độ cao lớn nhất?
Hướng dẫn giải:
Đang cập nhật...
-----------------------------------------------
---> Xem thêm: Giải Toán 12 trang 13 tập 1 Kết nối tri thức
Lời giải Toán 12 trang 12 Tập 1 Kết nối tri thức với các câu hỏi nằm trong Bài 1 Tính đơn điệu và cực trị của hàm số, được VnDoc biên soạn và đăng tải!
