Giải Toán 12 trang 28 tập 1 Kết nối tri thức
Giải Toán 12 trang 28 Tập 1
Giải Toán 12 trang 28 Tập 1 Kết nối tri thức hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 12 Kết nối tri thức tập 1 trang 28.
Luyện tập 1 trang 28 SGK Toán 12 tập 1 Kết nối
Khảo sát sự biến thiên và vẽ đồ thị của hàm số y = −2x3 + 3x2 – 5x.
Hướng dẫn giải:
1. Tập xác định của hàm số: 
\(\mathbb{R}\)
2. Sự biến thiên:
- Ta có: y' = - 6x2 + 6x - 5. Vậy y' < 0 với mọi x ∈ \(\mathbb{R}\).
- Hàm số nghịch biến trên khoảng (- ∞; + ∞).
- Hàm số không có cực trị.
- Giới hạn tại vô cực:
\(\lim_{x\rightarrow - \infty} y =\lim_{x\rightarrow - \infty} \left ( − 2x^3 + 3x^2 – 5x \right ) = + \infty\)
\(\lim_{x\rightarrow + \infty} y =\lim_{x\rightarrow + \infty} \left ( − 2x^3 + 3x^2 – 5x \right ) = - \infty\)
- Bảng biến thiên:
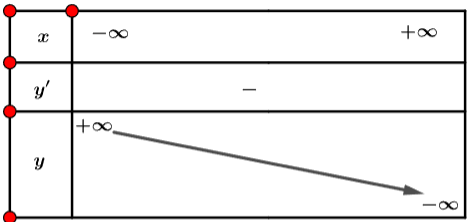
3. Đồ thị:
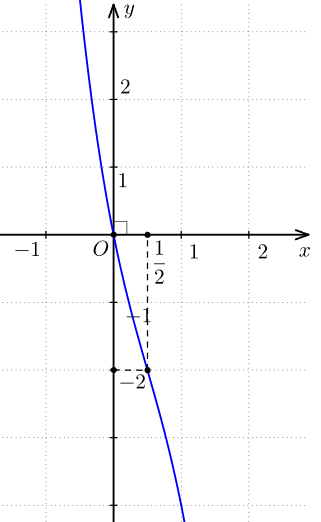
Giao điểm của đồ thị hàm số với trục tung là điểm (0; 0).
Điểm (1; - 4) thuộc đồ thị hàm số.
Đồ thị hàm số có tâm đối xứng là điểm \(\left(\frac{1}{2};-2\right)\).
-----------------------------------------------
---> Xem thêm: Giải Toán 12 trang 29 tập 1 Kết nối tri thức
Lời giải Toán 12 trang 28 Tập 1 Kết nối tri thức với các câu hỏi nằm trong Bài 4: Khảo sát sự biến thiên và vẽ đồ thị của hàm số, được VnDoc biên soạn và đăng tải!
