Giải Toán 12 trang 37 tập 1 Chân trời sáng tạo
Giải Toán 12 trang 37 Tập 1
- Bài 1 trang 37 SGK Toán 12 tập 1 Chân trời
- Bài 2 trang 37 SGK Toán 12 tập 1 Chân trời
- Bài 3 trang 37 SGK Toán 12 tập 1 Chân trời
- Bài 4 trang 37 SGK Toán 12 tập 1 Chân trời
- Bài 5 trang 37 SGK Toán 12 tập 1 Chân trời
- Bài 6 trang 37 SGK Toán 12 tập 1 Chân trời
- Bài 7 trang 37 SGK Toán 12 tập 1 Chân trời
Giải Toán 12 trang 37 Tập 1 hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 12 Chân trời sáng tạo tập 1 trang 37.
Bài 1 trang 37 SGK Toán 12 tập 1 Chân trời
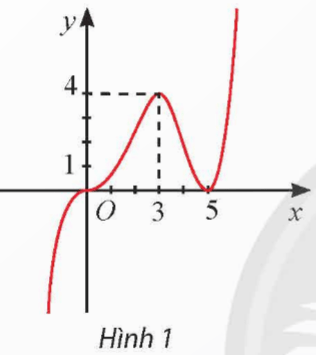
Cho hàm số y = f(x) có đồ thị như Hình 1. Hàm số y = f(x) đồng biến trên khoảng
|
A. (5; + ∞). B. (3; 5). C. (0; 5). D. (3; + ∞). |
 |
Hướng dẫn giải:
Đáp án đúng: A
Hàm số y = f(x) đồng biến trên các khoảng 
\((-\infty ; 3)\) và \((5;+\infty )\)
Bài 2 trang 37 SGK Toán 12 tập 1 Chân trời
Cho hàm số y = f(x) có đồ thị như Hình 1. Hàm số đạt cực đại tại
|
A. x = 0. B. x = 3. C. x = 4. D. x = 5. |
|
Hướng dẫn giải:
Đáp án đúng: B
Hàm số y = f(x) có f'(x) > 0 trên khoảng \((-\infty ; 3)\) và f'(x) < 0 trên khoảng (3; 5) nên đạt cực đại tại x = 3.
Bài 3 trang 37 SGK Toán 12 tập 1 Chân trời
Cho hàm số \(y = \frac{x^{2}-4x+1 }{x-4}\). Trong các khẳng định sau, khẳng định nào đúng?
A. Hàm số đạt cực tiểu tại x = 3, giá trị cực tiểu là y = 2.
B. Hàm số đạt cực tiểu tại x = 5, giá trị cực tiểu là y = 6.
C. Hàm số đạt cực tiểu tại x = 3, giá trị cực tiểu là y = 6.
D. Hàm số đạt cực tiểu tại x = 5, giá trị cực tiểu là y = 2.
Hướng dẫn giải:
Đáp án đúng: B
Xét hàm số, TXĐ: \(\mathbb{R} \setminus \left \{ 4 \right \}\)
Ta có: \(y'=1-\frac{1}{\left(x-4\right)^2}\)
y' = 0 ⇔ x = 5 hoặc x = 3
Lập bảng biến thiên:
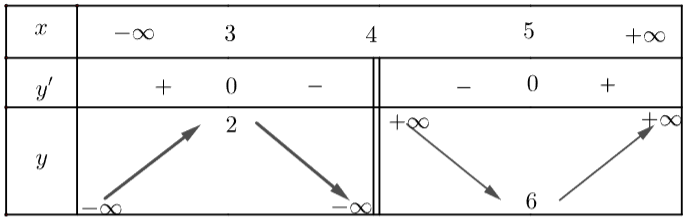
Vậy y đạt cực tiểu tại x = 5 và yCT = 6.
Bài 4 trang 37 SGK Toán 12 tập 1 Chân trời
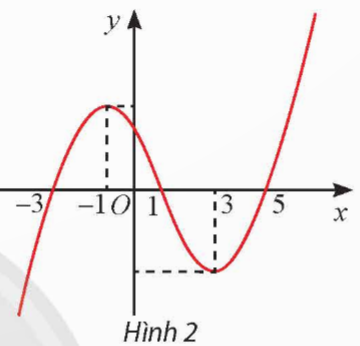
Đạo hàm của hàm số y = f(x) là hàm số có đồ thị được cho trong Hình 2. Hàm số y = f(x) nghịch biến trên khoảng
|
A. (– 1; 3). B. (– 3; 1). C. (1; 5). D. (3; + ∞). |
 |
Hướng dẫn giải:
Đáp án đúng: C
f'(x) < 0 khi thuộc các khoảng \((-\infty; -3)\) và (1; 5) nên f(x) nghịch biến trên các khoảng đó.
Bài 5 trang 37 SGK Toán 12 tập 1 Chân trời
Giá trị nhỏ nhất của hàm số \(y = \sqrt {{x^2} + 2x + 3}\) trên đoạn [–2; 3] là
A. \(\sqrt 3\)
B. \(\sqrt {30}\)
C. \(\sqrt 2\)
D. 0
Hướng dẫn giải:
Đáp án đúng: C
\(y'=\frac{x+1}{\sqrt{x^2+2x+3}}\); y' = 0 => x = - 1.
\(f\left(-2\right)=\sqrt{3};\ f\left(-1\right)=\sqrt{2};\ f\left(3\right)=3\sqrt{2}\)
Vậy \(\underset{[-2;3]}{\min} y=y(-1)=\sqrt{2}\)
Bài 6 trang 37 SGK Toán 12 tập 1 Chân trời
Tiệm cận xiên của đồ thị hàm số \(y = \frac{{2{x^3} + 3{x^2} - 3}}{{{x^2} - 1}}\) là đường thẳng có phương trình:
|
A. y = 2x + 3 B. y = x + 3 |
C. y = 2x + 1 D. y = x + 1 |
Hướng dẫn giải:
Đáp án đúng: A
Ta có: \(a=\lim_{x \rightarrow +\infty } \frac{{2{x^3} + 3{x^2} - 3}}{{{x^3} - x}} = 2\) và \(b= \lim_{x \rightarrow +\infty } \left ( \frac{{2{x^3} + 3{x^2} - 3}}{{{x^2} - 1}} -2x\right ) = 3\)
Suy ra đường thẳng y = 2x + 3 là tiệm cận xiên của đồ thị hàm số.
Bài 7 trang 37 SGK Toán 12 tập 1 Chân trời
Tiệm cận đứng của đồ thị hàm số \(y = \frac{{ - 2x + 3}}{{5x + 1}}\) là đường thẳng có phương trình
|
A. B. |
C. D. |
Hướng dẫn giải:
Đáp án đúng: B
Ta có: \(\lim_{x\rightarrow -\frac{1}{5}^+ } \frac{{ - 2x + 3}}{{5x + 1}}=+\infty\); \(\lim_{x\rightarrow -\frac{1}{5}^- } \frac{{ - 2x + 3}}{{5x + 1}}=-\infty\)
-----------------------------------------------
---> Xem thêm: Giải Toán 12 trang 38 tập 1 Chân trời sáng tạo
Lời giải Toán 12 trang 37 Tập 1 Chân trời sáng tạo với các câu hỏi nằm trong Bài tập cuối chương 1, được VnDoc biên soạn và đăng tải!
