Giải Toán 12 trang 45 tập 1 Cánh diều
Giải Toán 12 trang 45 Cánh diều Tập 1
Giải Toán 12 trang 45 Tập 1 hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 12 Cánh diều tập 1 trang 45.
Bài 1 trang 45 SGK Toán 12 tập 1
Cho hàm số 
có đồ thị hàm số y = f'(x) cho ở Hình 31.
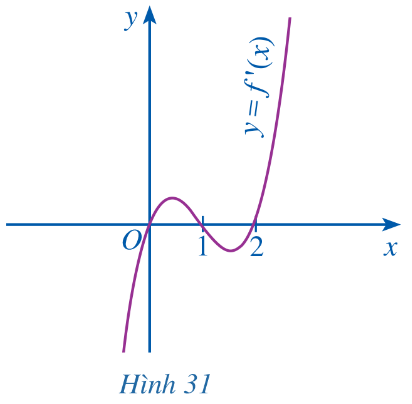
Hàm số y = f(x) đồng biến trên khoảng:
| A. (– ∞; 0) | B. (0; 1) | C. (0; 2) | D. (1; 2) |
Hướng dẫn giải:
Đáp án đúng: B
Bài 2 trang 45 SGK Toán 12 tập 1
Số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số là:
| A. 0 | B. 1 | C. 2 | D. 3 |
Hướng dẫn giải:
Đáp án đúng: C
Bài 3 trang 45 SGK Toán 12 tập 1
Hàm số nào có đồ thị như Hình 32?
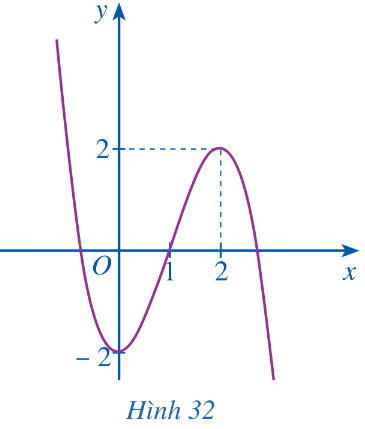
A. y = – x3 + 3x – 2 B. y = – x3 – 2 | C. y = – x3 + 3x2 – 2 D. y = x3 – 3x – 2 |
Hướng dẫn giải:
Đáp án đúng: C
-----------------------------------------------
---> Xem thêm: Giải Toán 12 trang 46 tập 1 Cánh diều
Lời giải Toán 12 trang 45 Tập 1 Cánh diều với các câu hỏi nằm trong Bài tập cuối chương 1, được VnDoc biên soạn và đăng tải!
