Toán 12 Chân trời sáng tạo bài 1: Vectơ và các phép toán trong không gian
Giải bài tập Toán 12 CTST bài 1
- Giải Toán 12 trang 41 Chân trời
- Giải Toán 12 trang 42 Chân trời
- Giải Toán 12 trang 43 Chân trời
- Giải Toán 12 trang 44 Chân trời
- Giải Toán 12 trang 45 Chân trời
- Giải Toán 12 trang 46 Chân trời
- Giải Toán 12 trang 47 Chân trời
- Giải Toán 12 trang 48 Chân trời
- Giải Toán 12 trang 49 Chân trời
- Giải Toán 12 trang 50 Chân trời
- Giải Toán 12 trang 51 Chân trời
Toán 12 Chân trời sáng tạo bài 1: Vectơ và các phép toán trong không gian được VnDoc.com tổng hợp gồm có hướng dẫn giải bài tập SGK Toán 12 Chân trời sáng tạo tập 1 các trang 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51
Giải Toán 12 trang 41 Chân trời
Hoạt động khởi động trang 41 SGK Toán 12 tập 1
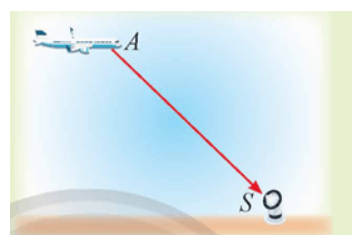
Trong không gian, làm thế nào để biểu diễn độ dịch chuyển tín hiệu vô tuyến từ máy bay đến trạm kiểm soát trên mặt đất.
Hoạt động khám phá 1 trang 41 SGK Toán 12 tập 1
Nhắc lại định nghĩa vectơ trong mặt phẳng. Có thể định nghĩa vectơ trong không gian như đã định nghĩa vectơ trong mặt phẳng không?
Xem lời giải Toán 12 trang 41
Giải Toán 12 trang 42 Chân trời
Thực hành 1 trang 42 SGK Toán 12 tập 1
Trong hoạt động khởi động, tìm vectơ biểu diễn độ dịch chuyển tín hiệu vô tuyến từ vị trí A của máy bay đến vị trí S của trạm kiểm soát.
Thực hành 2 trang 42 SGK Toán 12 tập 1
Cho hình chóp tứ giác đều S.ABCD.
a) Chỉ ra các vectơ có điểm đầu là S và điểm cuối là các đỉnh của đa giác đáy.
b) Tìm các vectơ có độ dài bằng độ dài của vectơ 
\(\overrightarrow{SA}\).
c) Tìm các vectơ đối của vectơ \(\overrightarrow{CB}\) .
Xem lời giải Toán 12 trang 42
Giải Toán 12 trang 43 Chân trời
Vận dụng 1 trang 43 SGK Toán 12 tập 1
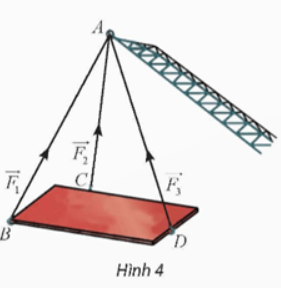
Trong Hình 4, cho biết ba vectơ \(\overrightarrow{F_{1} }, \overrightarrow{F_{2} }, \overrightarrow{F_{3} }\) biểu diễn lực căng của các sợi dây cáp AB, AC, AD tác dụng lên vật nặng. Giá của ba vectơ này có cùng nằm trên một mặt phẳng không?
Hoạt động khám phá 2 trang 43 SGK Toán 12 tập 1
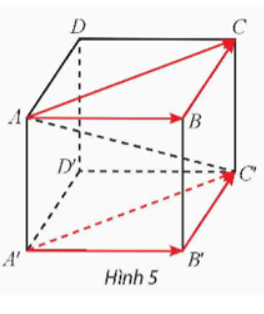
Cho hình hộp ABCD.A'B'C'D' (Hình 5).
a) Trong mặt phẳng (ABCD), tìm vectơ tổng \(\overrightarrow{AB} +\overrightarrow{BC}\).
Trong mặt phẳng (A'B'C'D'), tìm vectơ tổng \(\overrightarrow{A'B'} + \overrightarrow{B'C'}\).
b) Tìm mối liên hệ giữa các cặp vectơ \(\overrightarrow{AB}\) và \(\overrightarrow{A'B'}\), \(\overrightarrow{BC}\) và \(\overrightarrow{B'C'}\), \(\overrightarrow{AC}\) và \(\overrightarrow{A'C'}\).
c) Giải thích tại sao \(\overrightarrow{AB}\) + \(\overrightarrow{BC}\) = \(\overrightarrow{A'B'}\) + \(\overrightarrow{B'C'}\).
Xem lời giải Toán 12 trang 43
Giải Toán 12 trang 44 Chân trời
Hoạt động khám phá 3 trang 44 SGK Toán 12 tập 1
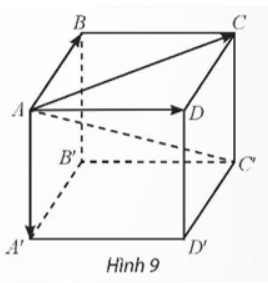
Cho hình hộp ABCD.A'B'C'D'.
a) Tìm các vectơ tổng \(\overrightarrow{AB} + \overrightarrow{AD} , \overrightarrow{AC} +\overrightarrow{AA'}\).
b) Dùng kết quả của câu a và tính chất kết hợp của phép cộng vectơ để chứng minh \(\overrightarrow{AB} +\overrightarrow{AD} + \overrightarrow{AA'} = \overrightarrow{AC'}\).
Xem lời giải Toán 12 trang 44
Giải Toán 12 trang 45 Chân trời
Thực hành 3 trang 45 SGK Toán 12 tập 1
Cho hình hộp ABCD.EFGH. Thực hiện các phép toán sau đây:
a) \(\overrightarrow {DA} + \overrightarrow {DC} + \overrightarrow {DH}\)
b) \(\overrightarrow {HE} + \overrightarrow {GC} + \overrightarrow {AB}\)
Hoạt động khám phá 4 trang 45 SGK Toán 12 tập 1
Cho hình hộp ABCD.A'B'C'D'
a) Trong mặt phẳng (ABCD), tìm vectơ hiệu\(\overrightarrow {AB} - \overrightarrow {AD}\).
Trong mặt phẳng (A'B'C'D'), tìm vectơ hiệu \(\overrightarrow {A'B'}- \overrightarrow {A'D'}\).
b) Tìm mối liên hệ giữa các cặp vectơ \(\overrightarrow {AB}\) và \(\overrightarrow {A'B'}\), \(\overrightarrow {AD}\) và \(\overrightarrow {A'D'}\), \(\overrightarrow {DB}\) và \(\overrightarrow {D'B'}\).
c) Giải thích tại sao \(\overrightarrow {AB}\) - \(\overrightarrow {AD}\) = \(\overrightarrow {A'B'}\) - \(\overrightarrow {A'D'}\).
Xem lời giải Toán 12 trang 45
Giải Toán 12 trang 46 Chân trời
Thực hành 4 trang 46 SGK Toán 12 tập 1
Cho tứ diện ABCD có M và N lần lượt là trung điểm của AB và CD. Tìm các vectơ:
a) \(\overrightarrow {BM}+\overrightarrow {AC}+\overrightarrow {ND}\);
b) \(\overrightarrow {AD}-\overrightarrow {AM}+\overrightarrow {NC}\).
Thực hành 5 trang 46 SGK Toán 12 tập 1
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng đơn vị. Tìm độ dài các vectơ sau đây:
a) \(\overrightarrow {a} = \overrightarrow {BA}+\overrightarrow {BC}+\overrightarrow {BB'}\)
b) \(\overrightarrow {b} = \overrightarrow {BC} - \overrightarrow {BA}+\overrightarrow {C'A}\)
Vận dụng 2 trang 46 SGK Toán 12 tập 1
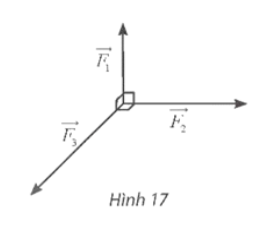
Ba lực \(\overrightarrow {F_{1} }, \overrightarrow {F_{2} }, \overrightarrow {F_{3} }\) cùng tác động vào một vật có phương đôi một vuông góc và có độ lớn lần lượt là 2 N; 3N; 4 N (Hình 17). Tính độ lớn hợp lực của ba lực đã cho.
Hoạt động khám phá 5 trang 46 SGK Toán 12 tập 1
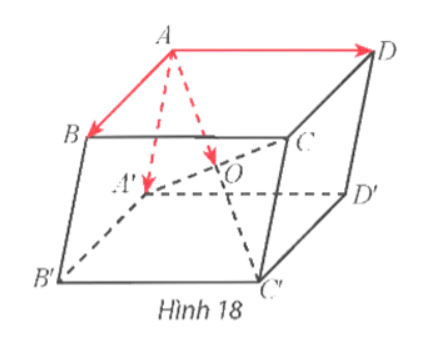
Cho hình hộp ABCD.A'B'C'D' có AC' và A'C cắt nhau tại O (Hình 18).
a) Tìm vectơ \(\overrightarrow {AB}+\overrightarrow {AD}+\overrightarrow {AA'}\).
b) Cho biết mối quan hệ giữa vectơ tìm được ở câu a và vectơ \(\overrightarrow {AO}\).
Xem lời giải Toán 12 trang 46
Giải Toán 12 trang 47 Chân trời
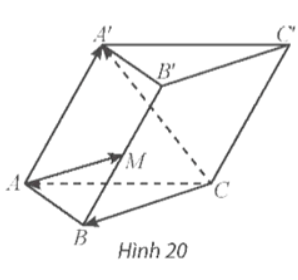
Thực hành 6 trang 47 SGK Toán 12 tập 1
Cho hình lăng trụ ABC.A'B'C' có M là trung điểm của BB' (Hình 20). Đặt \(\overrightarrow {CA}=\overrightarrow {a}\), −\(\overrightarrow {CB} = \overrightarrow {b}\), −\(\overrightarrow {CC'} = \overrightarrow {c}\). Chứng minh rằng \(\overrightarrow {AM} = \overrightarrow {b} - \overrightarrow {a} + \frac{1}{2} \overrightarrow {c}\).
Xem lời giải Toán 12 trang 47
Giải Toán 12 trang 48 Chân trời
Vận dụng 3 trang 48 SGK Toán 12 tập 1
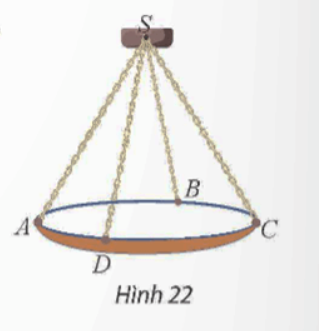
Một chiếc đèn chùm treo có khối lượng m = 5 kg được thiết kế với đĩa đèn được giữ bởi bốn đoạn xích SA, SB, SC, SD sao cho S.ABCD là hình chóp tứ giác đều có \(\widehat {ASC}\) = 60° (Hình 22).
a) Sử dụng công thức \(\overrightarrow {P} = m\overrightarrow {g}\) trong đó \(\overrightarrow {g}\) là vectơ gia tốc rơi tự do có độ lớn 10 m/s2, tìm độ lớn của trọng lực \(\overrightarrow {P}\) tác động lên chiếc đèn chùm.
b) Tìm độ lớn của lực căng cho mỗi sợi xích.
Hoạt động khám phá 6 trang 48 SGK Toán 12 tập 1
a) Nhắc lại định nghĩa góc giữa hai vectơ \(\overrightarrow {u}\) và \(\overrightarrow {v}\) trong mặt phẳng.
b) Làm thế nào để định nghĩa góc giữa hai vectơ \(\overrightarrow {u}\) và \(\overrightarrow {v}\) trong không gian.
Xem lời giải Toán 12 trang 48
Giải Toán 12 trang 49 Chân trời
Thực hành 7 trang 49 SGK Toán 12 tập 1
Cho hình lập phương ABCD.A′B′C′D′. Xác định góc \((\overrightarrow {AC} ,\overrightarrow {B'D'} ),(\overrightarrow {A'A} ,\overrightarrow {CB'} )\)
Hoạt động khám phá 7 trang 49 SGK Toán 12 tập 1
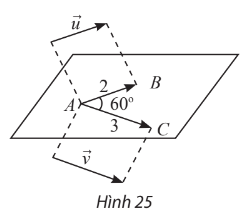
Trong không gian, cho \(\overrightarrow u và \overrightarrow v\) thoả mãn \(|\overrightarrow u | = 2 , |\overrightarrow v | = 3\). Lấy một điểm A bất kì, gọi B và C là hai điểm sao cho \(\overrightarrow {AB} = \overrightarrow u , \overrightarrow {AC} = \overrightarrow v\) (Hình 24). Giả sử \(\widehat {BAC} = 60^\circ\)
a) Tính góc \((\overrightarrow u ,\overrightarrow v )\)
b) Trong mặt phẳng (ABC), tính tích vô hướng \(\overrightarrow {AB} .\overrightarrow {AC}\)
Xem lời giải Toán 12 trang 49
Giải Toán 12 trang 50 Chân trời
Thực hành 8 trang 50 SGK Toán 12 tập 1
Cho hình lập phương ABCD.A′B′C′D′ có cạnh bằng 1.
a) Tính các tích vô hướng: \(\overrightarrow {AB} .\overrightarrow {A'C'} , \overrightarrow {AB} .\overrightarrow {CC'}\)
b) Tính góc \((\overrightarrow {AC} .\overrightarrow {AC'} )\) (kết quả làm tròn đến phút)
Vận dụng 4 trang 50 SGK Toán 12 tập 1
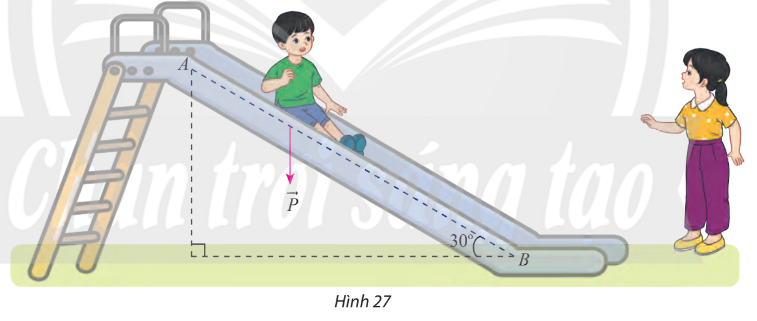
Một em nhỏ cân nặng m = 25 kg trượt trên cầu trượt dài 3,5m. Biết rằng, cầu trượt có góc nghiêng so với phương nằm ngang là \(30^\circ\) (Hình 27).
a) Tính độ lớn của trọng lực \(\overrightarrow P = m\overrightarrow g\) tác dụng lên em nhỏ, cho biết vectơ gia tốc rơi tự do \(\overrightarrow g\) có độ lớn 9,8 m/s2
b) Cho biết công A (J) sinh bởi một lực \(\overrightarrow F\) có độ dịch chuyển \(\overrightarrow d\) được tính bởi công thức \(A = \overrightarrow F .\overrightarrow d\). Hãy tính công sinh bởi trọng lực \(\overrightarrow P\) khi em nhỏ trượt hết chiều dài cầu trượt.
Bài 1 trang 50 SGK Toán 12 tập 1
Cho hình hộp ABCD.A′B′C′D′. Chứng minh rằng:
a) \(\overrightarrow {AB} + \overrightarrow {B'C'} + \overrightarrow {DD'} = \overrightarrow {AC'}\)
b) \(\overrightarrow {DB'} + \overrightarrow {D'D} + \overrightarrow {BD'} = \overrightarrow {BB'}\)
c) \(\overrightarrow {AC} + \overrightarrow {BA'} + \overrightarrow {DB} + \overrightarrow {C'D} = \overrightarrow 0\)
Xem lời giải Toán 12 trang 50
Giải Toán 12 trang 51 Chân trời
Bài 2 trang 51 SGK Toán 12 tập 1
Cho hình bình hành ABCD. Gọi S là một điểm không thuộc mặt phẳng chứa hình bình hành. Chứng minh rằng \(\overrightarrow {SA} + \overrightarrow {SC} = \overrightarrow {SB} + \overrightarrow {SD}\)
Bài 3 trang 51 SGK Toán 12 tập 1
Ba lực có điểm đặt tại một đỉnh của hình lập phương, cùng phương với ba cạnh và cùng có cường độ là 5N. Tính cường độ của hợp lực.
Bài 4 trang 51 SGK Toán 12 tập 1
Cho hình chóp S.ABCD. Gọi I là trọng tâm của tam giác ABC và J là trọng tâm tam giác ADC. Chứng minh rằng \(2\overrightarrow {SA} + \overrightarrow {SB} + 2\overrightarrow {SC} + \overrightarrow {SD} = 3(\overrightarrow {SI} + \overrightarrow {SJ} )\)
Bài 5 trang 51 SGK Toán 12 tập 1
Cho hình lăng trụ tam giác ABC.A′B′C′ có \(\overrightarrow {AA'} = \overrightarrow a , \overrightarrow {AB} = \overrightarrow b ,\overrightarrow {AC} = \overrightarrow c\). Chứng minh rằng \(\overrightarrow {B'C} = \overrightarrow c - \overrightarrow a - \overrightarrow b\) và \(\overrightarrow {BC'} = \overrightarrow a - \overrightarrow b + \overrightarrow c\)
Bài 6 trang 51 SGK Toán 12 tập 1
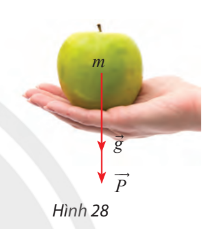
Nếu một vật có khối lượng m (kg) thì lực hấp dẫn \(\overrightarrow P\) của Trái Đất tác dụng lên vật được xác định theo công thức \(\overrightarrow P = m\overrightarrow g\), trong đó \(\overrightarrow g\) là gia tốc rơi tự do có độ lớn 9,8 m/s2. Tính độ lớn của lực hấp dẫn của Trái Đất tác dụng lên một quả táo có khối lượng 102 gam (Hình 28).
Bài 7 trang 51 SGK Toán 12 tập 1
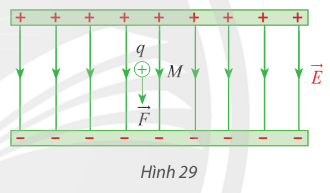
Trong điện trường đều, lực tĩnh điện \(\overrightarrow F\) (đơn vị: N) tác dụng lên điện tích điểm có điện tích q (đơn vị: C) được tính theo công thức \(\overrightarrow F = q.\overrightarrow E\), trong đó \(\overrightarrow E\) là cường độ điện trường (đơn vị: N/C). Tính độ lớn của lực tĩnh điện tác dụng lên điện tích điểm khi \(q = {10^{ - 9}}C\) và độ lớn điện trường \(E = {10^5}\) N/C (Hình 29).
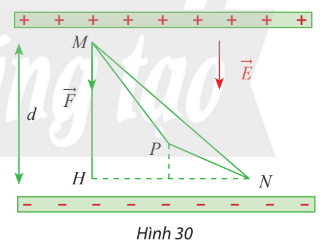
Bài 8 trang 51 SGK Toán 12 tập 1
Một lực tĩnh điện \(\overrightarrow F\) tác động lên điện tích điểm M trong điện trường đều làm cho M dịch chuyển theo đường gấp khúc MNP (Hình 30). Biết \(q = {2.10^{ - 12}}C\), vectơ điện trường có độ lớn \(E = 1,{8.10^5}\) N/C và d = MH = 5mm. Tính công A sinh bởi lực tĩnh điện \(\overrightarrow F\).
Xem lời giải Toán 12 trang 51
Bài tiếp theo: Toán 12 Chân trời sáng tạo bài 2: Toạ độ của vectơ trong không gian
