VnDoc.com

Giải Toán 12 trang 47 tập 1 Cánh diều

Bài trước

Bài sau

Giải Toán 12 trang 47 Cánh diều Tập 1

Bài 8 trang 47 SGK Toán 12 tập 1
Bài 9 trang 47 SGK Toán 12 tập 1
Bài 10 trang 47 SGK Toán 12 tập 1
Bài 11 trang 47 SGK Toán 12 tập 1

Giải Toán 12 trang 47 Tập 1 hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 12 Cánh diều tập 1 trang 47.

Bài 8 trang 47 SGK Toán 12 tập 1

Tìm giá trị nhỏ nhất và giá trị lớn nhất của mỗi hàm số sau:

a) f(x) = 2x³ − 6x trên đoạn [− 1; 3]

b) $f\left( x \right) = \frac{{{x^2} + 3x + 6}}{{x + 2}}$ $f\left( x \right) = \frac{{{x^2} + 3x + 6}}{{x + 2}}$ trên đoạn [1; 5]

c) $f\left( x \right) = \frac{{ln\left( {x + 1} \right)}}{{x + 1}}$ $f\left( x \right) = \frac{{ln\left( {x + 1} \right)}}{{x + 1}}$ trên đoạn [0; 3]

d) f(x) = 2sin3x + 7x + 1 trên đoạn $\left[ {\frac{{ - \pi }}{2};\frac{\pi }{2}} \right]$ $\left[ {\frac{{ - \pi }}{2};\frac{\pi }{2}} \right]$.

Hướng dẫn giải:

a) f(x) = 2x³ − 6x trên đoạn [− 1; 3]

Ta có: f'(x) = 6x² - 6

f'(x) = 0 ⇔ x = - 1 hoặc x = 1

f(- 1) = 4; f(1) = - 4; f(3) = 36

Vậy $\underset{[− 1; 3] }{\max} f(x)=36; \ \underset{[− 1; 3]}{\min} f(x)=-4$ $\underset{[− 1; 3] }{\max} f(x)=36; \ \underset{[− 1; 3]}{\min} f(x)=-4$

b) $f\left( x \right) = \frac{{{x^2} + 3x + 6}}{{x + 2}}$ $f\left( x \right) = \frac{{{x^2} + 3x + 6}}{{x + 2}}$ trên đoạn [1; 5]

Ta có: $f'\left(x\right)=\frac{x^2+4x}{\left(x+2\right)^2}$

f'(x) = 0 ⇔ x = - 4 hoặc x = 0

$f\left(1\right)=\frac{10}{3};\ \ f\left(5\right)=\frac{46}{7}$ $f\left(1\right)=\frac{10}{3};\ \ f\left(5\right)=\frac{46}{7}$

Vậy $\underset{[1; 5] }{\max} f(x)=\frac{46}{7}; \ \underset{[1; 5]}{\min} f(x)= \frac{10}{3}$ $\underset{[1; 5] }{\max} f(x)=\frac{46}{7}; \ \underset{[1; 5]}{\min} f(x)= \frac{10}{3}$

c) $f\left( x \right) = \frac{{\ln\left( {x + 1} \right)}}{{x + 1}}$ $f\left( x \right) = \frac{{\ln\left( {x + 1} \right)}}{{x + 1}}$ trên đoạn [0; 3]

Ta có: $f'\left(x\right)=\frac{\ln(x+1)-1}{\left(x+1\right)^2}$

f'(x) = 0 ⇔ x = e - 1

$f\left(0\right)=0;\ \ f\left(e-1\right)=\frac{1}{e} ;\ \ f\left(3\right)=\frac{\ln4}{4}$ $f\left(0\right)=0;\ \ f\left(e-1\right)=\frac{1}{e} ;\ \ f\left(3\right)=\frac{\ln4}{4}$

Vậy $\underset{[0;3] }{\max} f(x)=\frac{1}{e}; \ \underset{[0;3]}{\min} f(x)= 0$ $\underset{[0;3] }{\max} f(x)=\frac{1}{e}; \ \underset{[0;3]}{\min} f(x)= 0$

d) f(x) = 2sin3x + 7x + 1 trên đoạn $\left[ {\frac{{ - \pi }}{2};\frac{\pi }{2}} \right]$ $\left[ {\frac{{ - \pi }}{2};\frac{\pi }{2}} \right]$

Ta có: f'(x) = 6cos3x + 7

f'(x) = 0 ⇔ $\cos3x=-\frac{7}{6}$ $\cos3x=-\frac{7}{6}$ => vô nghiệm

$f\left(-\frac{\pi}{2}\right)=3-\frac{7\pi}{2};\ f\left(\frac{\pi}{2}\right)=-1+\frac{7\pi}{2}$ $f\left(-\frac{\pi}{2}\right)=3-\frac{7\pi}{2};\ f\left(\frac{\pi}{2}\right)=-1+\frac{7\pi}{2}$

Vậy $\underset{[-\frac{\pi }{2};\frac{\pi }{2}] }{\max} f(x)=-1+\frac{7\pi }{2}; \ \underset{[-\frac{\pi }{2};\frac{\pi }{2}]}{\min} f(x)= 3-\frac{7\pi }{2}$ $\underset{[-\frac{\pi }{2};\frac{\pi }{2}] }{\max} f(x)=-1+\frac{7\pi }{2}; \ \underset{[-\frac{\pi }{2};\frac{\pi }{2}]}{\min} f(x)= 3-\frac{7\pi }{2}$

Bài 9 trang 47 SGK Toán 12 tập 1

Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau

a) y = x³ - 3x² + 2

b) y = - x³ + 3x² - 6x

c) $y = \frac{{3x - 2}}{{x - 2}}$ $y = \frac{{3x - 2}}{{x - 2}}$

d) $y = \frac{x}{{2x + 3}}$ $y = \frac{x}{{2x + 3}}$

e) $y = \frac{{{x^2} + 2x + 4}}{x}$ $y = \frac{{{x^2} + 2x + 4}}{x}$

g) $y = \frac{{{x^2} + 4x + 3}}{{x + 2}}\;$ $y = \frac{{{x^2} + 4x + 3}}{{x + 2}}\;$

Hướng dẫn giải:

a) y = x³ - 3x² + 2

b) y = - x³ + 3x² - 6x

c) $y = \frac{{3x - 2}}{{x - 2}}$ $y = \frac{{3x - 2}}{{x - 2}}$

d) $y = \frac{x}{{2x + 3}}$ $y = \frac{x}{{2x + 3}}$

e) _{$y = \frac{{{x^2} + 2x + 4}}{x}$}

g) $y = \frac{{{x^2} + 4x + 3}}{{x + 2}}\;$ $y = \frac{{{x^2} + 4x + 3}}{{x + 2}}\;$

Bài 10 trang 47 SGK Toán 12 tập 1

Một trang sách có dạng hình chữ nhật với diện tích là 384 cm². Sau khi để lề trên và lề dưới đều là 3 cm, để lề trái và lề phải đều là 2 cm. Phần còn lại của trang sách được in chữ. Kích thước tối ưu của trang sách là bao nhiêu để phần in chữ trên trang sách có diện tích lớn nhất?

Hướng dẫn giải:

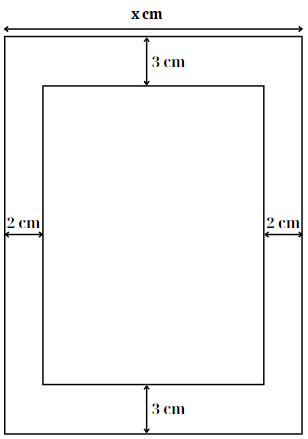
Gọi chiều rộng của trang sách là x (cm) (4 < x < 64)

Chiều dài của trang sách là $\frac{384}{x}$ $\frac{384}{x}$ (cm)

Chiều rộng của phần in chữ là: x - 4 (cm)

Chiều dài của phần bìa chữ là: $\frac{384}{x}-6=\frac{384-6x}{x}$ $\frac{384}{x}-6=\frac{384-6x}{x}$ (cm)

Diện tích của phần in chữ là: $\left(x-4\right).\frac{384-6x}{x}$ $\left(x-4\right).\frac{384-6x}{x}$ (cm²)

Xét hàm số $y=S\left(x\right)=\left(x-4\right).\frac{384-6x}{x}=\frac{6\left(-x^2+68x-256\right)}{x}$ $y=S\left(x\right)=\left(x-4\right).\frac{384-6x}{x}=\frac{6\left(-x^2+68x-256\right)}{x}$

Ta có: $y'=\frac{-6\left(x^2-256\right)}{x^2}$

y' = 0 ⇔ x = 16 (vì x > 0)

Lập bảng biến thiên của hàm số y = S(x)

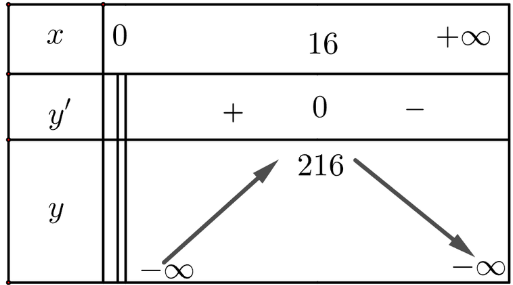
Từ bảng biến thiên ta có: $\underset{(0;+\infty)}{\max} y=y(16)=216$ $\underset{(0;+\infty)}{\max} y=y(16)=216$

Vậy kích thước tối ưu của trang sách là 16 cm và 24 cm thì phần in chữ trên trang sách có diện tích lớn nhất.

Bài 11 trang 47 SGK Toán 12 tập 1

Một người nông dân có 15 000 000 đồng để làm một hàng rào hình chữ E dọc theo một con sông bao quanh hai khu đất trồng rau có dạng hai hình chữ nhật bằng nhau (Hình 35). Đối với mặt hàng rào song song với bờ sông thì chi phí nguyên vật liệu là 60 000 đồng/mét, còn đối với ba mặt hàng rào song song nhau thì chi phí nguyên vật liệu là 50 000 đồng/mét, mặt giáp với bờ sông không phải rào. Tìm diện tích lớn nhất của hai khu đất thu được sau khi làm hàng rào.