Giải Toán 12 trang 9 tập 1 Chân trời sáng tạo
Giải Toán 12 trang 9 Tập 1
Giải Toán 12 trang 9 Tập 1 hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 12 Chân trời sáng tạo tập 1 trang 9.
Thực hành 2 trang 9 SGK Toán 12 tập 1 Chân trời
Xét tính đơn điệu của các hàm số sau:
a) f(x) = x3 – 6x2 + 9x;
b) 
\(g(x)=\frac{1}{x}\)
Hướng dẫn giải:
a) Xét hàm số f(x) = x3 – 6x2 + 9x
Tập xác định: D = \(\mathbb{R}\)
Ta có: f'(x) = 3x2 - 12x + 9;
f'(x) = 0 ⇔ x = 1 hoặc x = 3.
Bảng biến thiên:
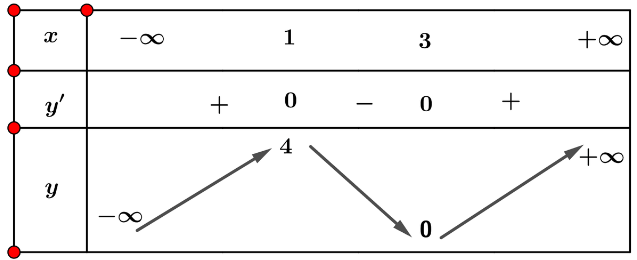
Vậy hàm số đồng biến trên các khoảng \((-\infty ; 1)\) và \((3; + \infty)\), nghịch biến trên khoảng (1; 3)
b) Xét hàm số \(g(x)=\frac{1}{x}\)
Tập xác định của hàm số: \(D=\mathbb{R} \setminus \left \{ 0\right \}\)
Ta có: \(g'\left(x\right)\ =-\frac{1}{x^2}<0, \forall x\ne 0\)
Vậy hàm số nghịch biến trên các khoảng \((-\infty ;0)\) và \((0; + \infty)\).
Thực hành 3 trang 9 SGK Toán 12 tập 1 Chân trời
Chứng minh rằng hàm số f(x) = 3x – sinx đồng biến trên ℝ.
Hướng dẫn giải:
Xét hàm số f(x) = 3x – sinx
Tập xác định: \(D=\mathbb{R}\)
Ta có: f'(x) = 3 - cosx
Do \(-1 \le \cos x \le 1\)
\(\Leftrightarrow 2 \le 3 - \cos x \le 4\)
⇔ f'(x) > 0 với mọi x
Vậy hàm số đồng biến trên ℝ.
Vận dụng 1 trang 9 SGK Toán 12 tập 1 Chân trời
Hãy trả lời câu hỏi trong phần khởi động (trang 6) bằng cách xét dấu đạo hàm của hàm số h(t) = 6t3 – 81t2 + 324t với 0 ≤ t ≤ 8.
Hướng dẫn giải:
Đang cập nhật...
-----------------------------------------------
---> Xem thêm: Giải Toán 12 trang 10 tập 1 Chân trời sáng tạo
Lời giải Toán 12 trang 9 Tập 1 Chân trời sáng tạo với các câu hỏi nằm trong Bài 1 Tính đơn điệu và cực trị của hàm số, được VnDoc biên soạn và đăng tải!
