Giải Toán 12 trang 62 tập 1 Kết nối tri thức

Giải Toán 12 trang 62 Tập 1 Kết nối tri thức hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 12 Kết nối tri thức tập 1 trang 62.

Luyện tập 2 trang 62 SGK Toán 12 tập 1 Kết nối

Tìm tọa độ của điểm N trong Hình 2.39.

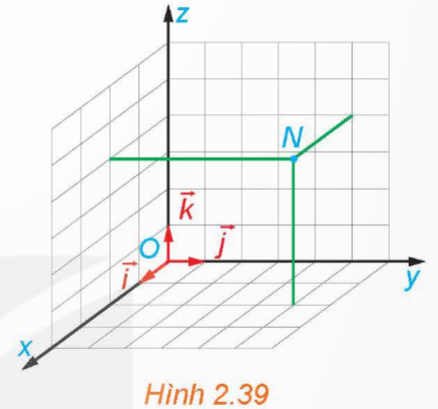
Hướng dẫn giải:

Áp dụng quy tắc hình hộp, ta có:

\(\overrightarrow{ON} = 2\overrightarrow{i} +5\overrightarrow{j} +4\overrightarrow{k}\)

Vậy tọa độ của điểm N là (2; 5; 4)

Luyện tập 3 trang 62 SGK Toán 12 tập 1 Kết nối

Trong Ví dụ 3, hãy xác định tọa độ của các điểm B, D và C'.

VD3: Trong không gian Oxyz, cho hình hộp chữ nhật ABCD.A'B'C'D' có đỉnh A' trùng với gốc O và các đỉnh D', B', A lần lượt thuộc các tia Ox, Oy, Oz (H.2.40). Giả sử đỉnh C có tọa độ là (2; 3; 5) đối với hệ tọa độ Oxyz.

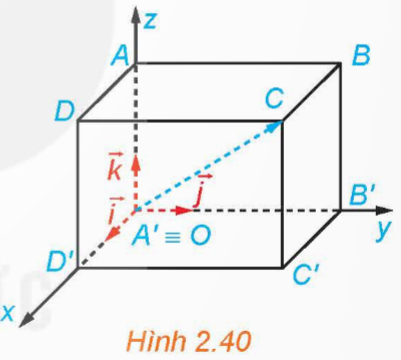
Hướng dẫn giải:

Ta có ABB'A' là hình bình hành nên \(\overrightarrow{OB}=\overrightarrow{OB'}+\overrightarrow{OA}=3\overrightarrow{j}+5\overrightarrow{k}\)

Suy ra điểm B có tọa độ là (0; 3; 5)

Tương tự ta có:

\(\overrightarrow{OD}=\overrightarrow{OD'}+\overrightarrow{OA}=2\overrightarrow{i}+5\overrightarrow{k}\) => điểm D có tọa độ là (2; 0; 5)

\(\overrightarrow{OC'}=\overrightarrow{OD'}+\overrightarrow{OB'}=2\overrightarrow{i}+3\overrightarrow{j}\) => điểm C' có tọa độ là (2; 3; 0)

Vận dụng 1 trang 62 SGK Toán 12 tập 1 Kết nối

Trong tình huống mở đầu, hãy chọn một hệ tọa độ phù hợp và xác định tọa độ của chiếc bóng đèn đối với hệ tọa độ đó.

Hướng dẫn giải:

Chọn gốc tọa độ O là góc tường, các trục trùng với các mép tường: trục Ox hướng về bên trái, trục Oy hướng về bên phải và trục Oz hướng lên trần nhà.

Khi đó tọa độ của bóng đèn là (1; 1,5; 2).

Hoạt động 3 trang 62 SGK Toán 12 tập 1 Kết nối

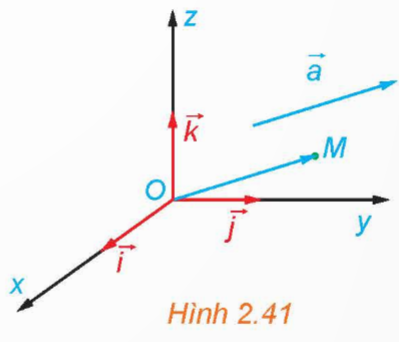
Trong không gian Oxyz, cho vectơ \(\overrightarrow{a}\) tùy ý (H.2.41). Lấy điểm M sao cho \(\overrightarrow{OM} =\overrightarrow{a}\) và giải thích vì sao có bộ ba số (x; y; z) sao cho \(\overrightarrow{a}=x\overrightarrow{i}+y\overrightarrow{j}+z\overrightarrow{k}\).

Hướng dẫn giải:

Gọi tọa độ của điểm M là (x; y; z).

Khi đó \(\overrightarrow{OM}=x\overrightarrow{i}+y\overrightarrow{j}+z\overrightarrow{k}\)

Suy ra \(\overrightarrow{a}=x\overrightarrow{i}+y\overrightarrow{j}+z\overrightarrow{k}\)

-----------------------------------------------

---> Bài tiếp theo: Giải Toán 12 trang 63 tập 1 Kết nối tri thức

Lời giải Toán 12 trang 62 Tập 1 Kết nối tri thức với các câu hỏi nằm trong Hệ trục tọa độ trong không gian, được VnDoc biên soạn và đăng tải!