Giải Toán 12 trang 16 tập 1 Chân trời sáng tạo

Giải Toán 12 trang 16 Tập 1 hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 12 Chân trời sáng tạo tập 1 trang 16.

Thực hành 1 trang 16 SGK Toán 12 tập 1 Chân trời

Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số:

a) f(x) = 2x³ – 9x² + 12x + 1 trên đoạn [0; 3];

b) \(g(x) = x + \frac{1}{x}\) trên khoảng (0; 5);

c) \(h(x) = x\sqrt{2 - x^{2}}\)

Hướng dẫn giải:

a) f(x) = 2x³ – 9x² + 12x + 1 trên đoạn [0; 3];

Ta có: f'(x) = 6x² - 18x + 12 = 6(x - 1)(x - 2)

f'(x) = 0 ⇔ \(\left [ \begin{array}{l} x= 1 \\ x = 2 \end{array} \right.\)

Lập bảng biến thiên của hàm số:

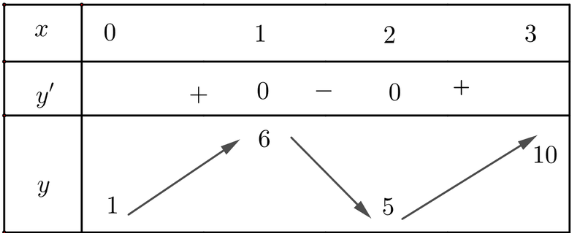
Từ bảng biến thiên ta được: \(\underset{ {[0;3]}}{\max} f(x) = 10,\ \underset{\mathbb{[0;3]}}{\min} f(x) =1\).

b) \(g(x) = x + \frac{1}{x}\) trên khoảng (0; 5);

Ta có: \(g'\left(x\right)=1-\frac{1}{x^2}\)

g'(x) = 0 ⇔ x = 1 (vì x ∈ (0; 5))

Lập bảng biến thiên của hàm số:

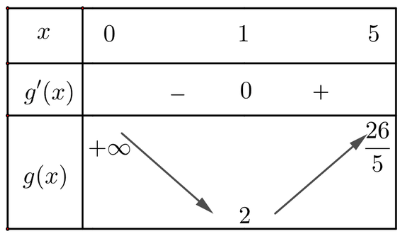
Từ bảng biến thiên ta được: \(\underset{ {(0;5)}}{\min} g(x) = 2\), hàm số không có giá trị lớn nhất

c) \(h(x) = x\sqrt{2 - x^{2}}\)

Đang cập nhật...

Vận dụng trang 16 SGK Toán 12 tập 1 Chân trời

Sử dụng đạo hàm và lập bảng biến thiên, trả lời câu hỏi trong mục khởi động (trang 14).

Hướng dẫn giải:

Ta có: \(y'\left(t\right)=\frac{135t^2-15}{\left(9t^2+1\right)}\)

y'(t) = 0 ⇔ \(t= \frac{ 1}{3}\) (vì t ≥ 0)

Lập bảng biến thiên của hàm số:

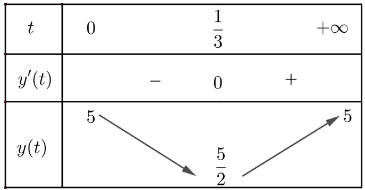
Vậy nồng độ oxygen trong nước cao nhất tại thời điểm t = 0 và thấp nhất tại thời điểm \(t= \frac{ 1}{3}\).

Hoạt động khám phá 2 trang 16 SGK Toán 12 tập 1 Chân trời

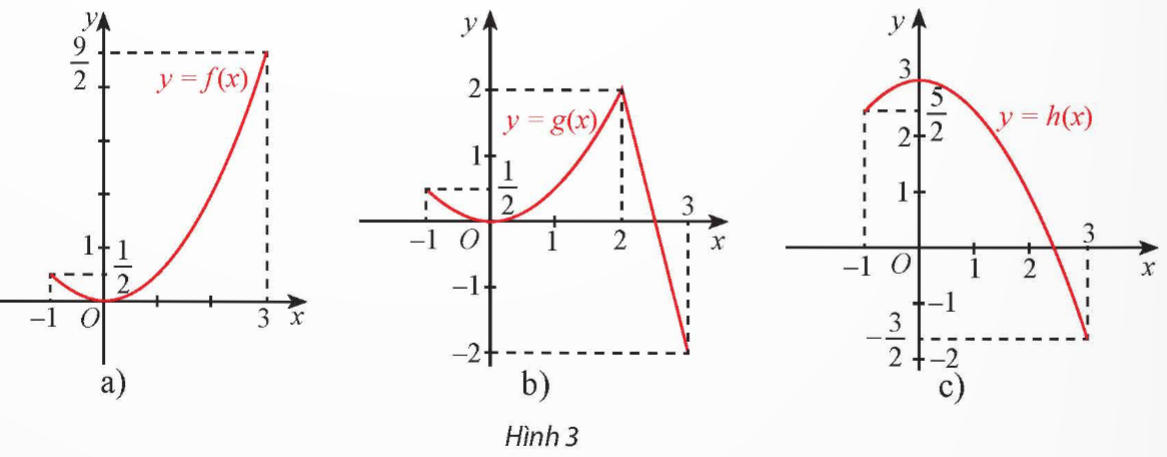
Hình 3 cho ta đồ thị của ba hàm số:

\(y = f(x)= \frac{1}{2} x^{2};\)

\(y = g(x)= \begin{cases} \frac{1}{2}x^{2} \ \ \ \ \ \ \ \ \ \ \text{ nếu } x\leq 2 \\ -4x+10 \ \text{ nếu } x\geq 2 \end{cases}\)

và \(y = h(x)=3-\frac{1}{2} x^{2}\) trên đoạn [−1; 3].

a) Hàm số nào đạt giá trị lớn nhất tại một điểm cực đại của nó?

b) Các hàm số còn lại đạt giá trị lớn nhất tại điểm nào?

Hướng dẫn giải:

a) Hàm số g(x) đạt giá trị cực đại tại x = 2 và \(\underset{[-1;3]}{\max} g(x)= g(2)=2\)

Hàm số h(x) đạt giá trị cực đại tại x = 0 và \(\underset{[-1;3]}{\max} h(x)= h(0)=3\)

b) Hàm số f(x) đạt giá trị lớn nhất tại x = 3.

-----------------------------------------------

---> Xem thêm: Giải Toán 12 trang 18 tập 1 Chân trời sáng tạo

Lời giải Toán 12 trang 16 Tập 1 Chân trời sáng tạo với các câu hỏi nằm trong Bài 2: Giá trị lớn nhất, giá trị nhỏ nhất của hàm số, được VnDoc biên soạn và đăng tải!