VnDoc.com

Giải Toán 12 trang 61 tập 1 Kết nối tri thức

Bài trước

Tải về

Bài sau

Giải Toán 12 trang 61 Tập 1

Câu hỏi trang 61 SGK Toán 12 tập 1 Kết nối
Luyện tập 1 trang 61 SGK Toán 12 tập 1 Kết nối
Hoạt động 2 trang 61 SGK Toán 12 tập 1 Kết nối

Giải Toán 12 trang 61 Tập 1 Kết nối tri thức hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 12 Kết nối tri thức tập 1 trang 61.

Câu hỏi trang 61 SGK Toán 12 tập 1 Kết nối

Góc căn phòng trong Hình 2.34 có gợi lên hình ảnh về hệ tọa độ Oxyz trong không gian hay không? Nếu có, hãy mô tả gốc tọa độ và các mặt phẳng tọa độ trong hình ảnh đó.

Hướng dẫn giải:

Góc căn phòng có gợi lên hình ảnh về hệ tọa độ Oxyz trong không gian.

Gốc tọa độ là góc phòng, các mặt phẳng tọa độ là hai mặt tường và mặt sàn.

Luyện tập 1 trang 61 SGK Toán 12 tập 1 Kết nối

Cho hình hộp chữ nhật ABCD.A'B'C'D'. Có thể lập một hệ tọa độ Oxyz có gốc O trùng với đỉnh C và các vectơ $\overrightarrow{i},\ \overrightarrow{j},\ \overrightarrow{k}$ $\vec{i}, \vec{j}, \vec{k}$ lần lượt cùng hướng với các vectơ $\overrightarrow{CB} , \overrightarrow{CD} , \overrightarrow{CC$ $\vec{C B}, \vec{C D}, \vec{C C^{'}}$ không? Giải thích vì sao.

Hướng dẫn giải:

Hình hộp chữ nhật ABCD.A'B'C'D' có các cạnh CB, CD, CC' đôi một vuông góc với nhau.

Các vectơ $\overrightarrow{CB} , \overrightarrow{CD} , \overrightarrow{CC$ $\vec{C B}, \vec{C D}, \vec{C C^{'}}$ có cùng điểm đầu là C.

Do đó có thể lập một hệ tọa độ Oxyz có gốc O trùng với đỉnh C và các vectơ $\overrightarrow{i},\ \overrightarrow{j},\ \overrightarrow{k}$ $\vec{i}, \vec{j}, \vec{k}$ lần lượt cùng hướng với các vectơ $\overrightarrow{CB} , \overrightarrow{CD} , \overrightarrow{CC$ $\vec{C B}, \vec{C D}, \vec{C C^{'}}$ .

Hoạt động 2 trang 61 SGK Toán 12 tập 1 Kết nối

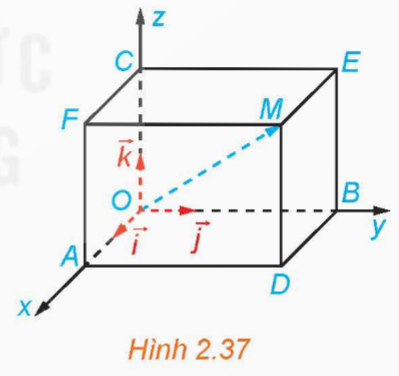
Trong không gian Oxyz, cho một điểm M không thuộc các mặt phẳng tọa độ. Vẽ hình hộp chữ nhật OADB.CFME có ba đỉnh A, B, C lần lượt thuộc các tia Ox, Oy, Oz (H.2.37).

a) Hai vectơ $\overrightarrow{OM}$ $\vec{O M}$ và $\overrightarrow{OA} +\overrightarrow{OB} +\overrightarrow{OC}$ $\vec{O A} + \vec{O B} + \vec{O C}$ có bằng nhau không?

b) Giải thích vì sao có thể viết $\overrightarrow{OM}=x\overrightarrow{i}+y\overrightarrow{j}+z\overrightarrow{k}$ $\vec{O M} = x \vec{i} + y \vec{j} + z \vec{k}$ với x, y, z là các số thực.

Hướng dẫn giải:

a) Áp dụng quy tắc hình hộp, ta có: $\overrightarrow{OM}=\overrightarrow{OA} +\overrightarrow{OB} +\overrightarrow{OC}$ $\vec{O M} = \vec{O A} + \vec{O B} + \vec{O C}$

b) Ta có các vectơ $\overrightarrow{i},\ \overrightarrow{j},\ \overrightarrow{k}$ $\vec{i}, \vec{j}, \vec{k}$ lần lượt cùng hướng với các vectơ $\overrightarrow{OA},\overrightarrow{OB}, \overrightarrow{OC}$ $\vec{O A}, \vec{O B}, \vec{O C}$

Do đó: $\overrightarrow{OA}=x\overrightarrow{i};\ \overrightarrow{OB}=y\overrightarrow{j};\ \overrightarrow{OC}=z\overrightarrow{k}$ $\vec{O A} = x \vec{i}; \vec{O B} = y \vec{j}; \vec{O C} = z \vec{k}$ với x, y, z là các số thực.

Vậy $\overrightarrow{OM}=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=x\overrightarrow{i}+y\overrightarrow{j}+z\overrightarrow{k}$ $\vec{O M} = \vec{O A} + \vec{O B} + \vec{O C} = x \vec{i} + y \vec{j} + z \vec{k}$

-----------------------------------------------

---> Bài tiếp theo: Giải Toán 12 trang 62 tập 1 Kết nối tri thức

Lời giải Toán 12 trang 61 Tập 1 Kết nối tri thức với các câu hỏi nằm trong Hệ trục tọa độ trong không gian, được VnDoc biên soạn và đăng tải!

Xem thêm các bài Tìm bài trong mục này khác:

Chia sẻ, đánh giá bài viết

1

27

Bài trước

Bài sau

Chia sẻ bởi:
Lê Jelar

Đóng Chỉ thành viên VnDoc PRO/PROPLUS tải được nội dung này!

Đóng

79.000 / tháng

Mua ngay

Đặc quyền các gói Thành viên

PRO

Phổ biến nhất

PRO+

Tải tài liệu Cao cấp 1 Lớp

Tải tài liệu Trả phí + Miễn phí

Xem nội dung bài viết

Trải nghiệm Không quảng cáo

Làm bài trắc nghiệm không giới hạn

Tìm hiểu thêm

Mua cả năm Tiết kiệm tới 48%

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!