Giải Toán 12 trang 30 tập 1 Cánh diều
Giải Toán 12 trang 30 Cánh diều Tập 1
Giải Toán 12 trang 30 Tập 1 hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 12 Cánh diều tập 1 trang 30.
Luyện tập 2 trang 30 SGK Toán 12 tập 1
Khảo sát sự biến thiên và vẽ đồ thị của mỗi hàm số sau:
a) y = – x3 + 3x – 2;
b) y = x3 + 3x2 + 3x + 1.
Hướng dẫn giải:
a) y = – x3 + 3x – 2
1) Tập xác định: 
\(\mathbb{R}\)
2) Sự biến thiên
- Giới hạn tại vô cực: \(\lim_{x \rightarrow +\infty} y = -\infty ; \ \lim_{x \rightarrow -\infty} y = +\infty\)
- Bảng biến thiên:
y' = – 3x2 + 3 với mọi x ∈ \(\mathbb{R}\).
y' = 0 ⇔ x = – 1 hoặc x = 1
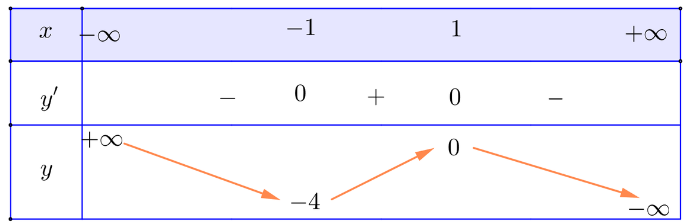
Hàm số đồng biến trên khoảng (– 1; 1), nghịch biến trên mỗi khoảng \((-\infty;-1)\) và \(( 1;+\infty)\)
Hàm số đạt cực đại tại x = 1, yCĐ = 0; hàm số đạt cực tiểu tại x = – 1, yCT = – 4.
3) Đồ thị
- Giao điểm của đồ thị với trục tung: (0; – 2)
- Giao điểm của đồ thị với trục hoành:
Giải phương trình – x3 + 3x – 2 = 0 ta được x = 1 hoặc x = – 2
Vậy đồ thị hàm số giao với trục hoành tại hai điểm (1; 0) và (– 2; 0)
- Đồ thị hàm số đi qua các điểm (– 1; – 4), (2; – 4)
Vậy đồ thị hàm số y = – x3 + 3x – 2 được cho ở hình bên dưới.
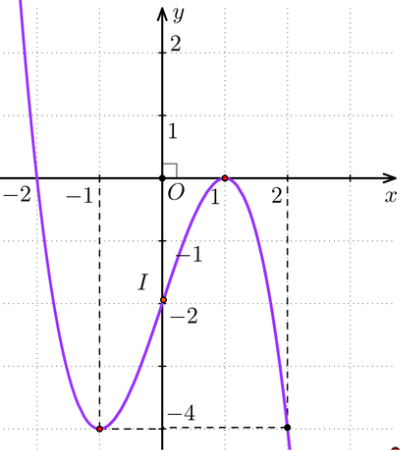
Tâm đối xứng của đồ thị hàm số đó là điểm I(0; – 2)
b) y = x3 + 3x2 + 3x + 1
1) Tập xác định: \(\mathbb{R}\)
2) Sự biến thiên
- Giới hạn tại vô cực: \(\lim_{x \rightarrow +\infty} y = +\infty ; \ \lim_{x \rightarrow -\infty} y =-\infty\)
- Bảng biến thiên:
y' = 3x2 + 6x + 3 > 0 với mọi x ∈ \(\mathbb{R}\).
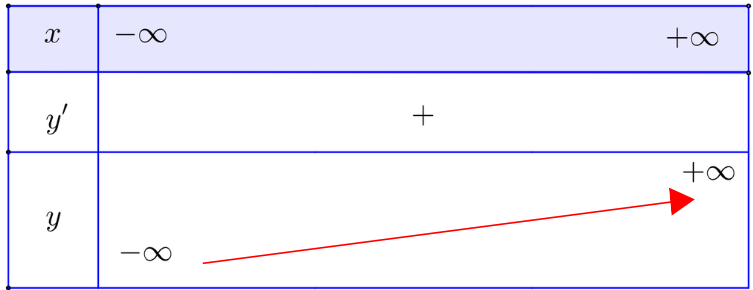
Hàm số đồng biến trên khoảng \(( -\infty;+\infty)\)
Hàm số không có cực trị.
3) Đồ thị
- Giao điểm của đồ thị với trục tung: (0; 1)
- Giao điểm của đồ thị với trục hoành:
Giải phương trình x3 + 3x2 + 3x + 1 = 0 ta được x = – 1
Vậy đồ thị hàm số giao với trục hoành tại điểm (– 1; 0)
- Đồ thị hàm số đi qua các điểm (– 2; – 1)
Vậy đồ thị hàm số y = x3 + 3x2 + 3x + 1 được cho ở hình bên dưới.
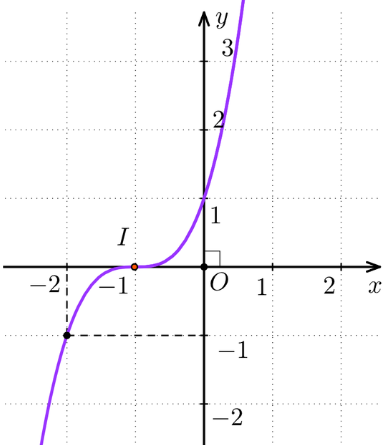
Tâm đối xứng của đồ thị hàm số đó là điểm I(– 1; 0)
-----------------------------------------------
---> Xem thêm: Giải Toán 12 trang 31 tập 1 Cánh diều
Lời giải Toán 12 trang 30 Tập 1 Cánh diều với các câu hỏi nằm trong Bài 4: Khảo sát sự biến thiên và vẽ đồ thị của hàm số, được VnDoc biên soạn và đăng tải!
