Toán 12 Cánh diều bài 1: Vectơ và các phép toán vectơ trong không gian
Giải bài tập Toán 12 CD bài 1
VnDoc.com xin gửi tới bạn đọc bài viết Toán 12 Cánh diều bài 1: Vectơ và các phép toán vectơ trong không gian để bạn đọc cùng tham khảo. Bài viết với hướng dẫn giải SGK Toán 12 Cánh diều tập 1 các trang 56, 57, 58, 59, 60, 61, 62, 63, 64.
Giải Toán 12 trang 56 Cánh diều
Câu hỏi khởi động trang 56 SGK Toán 12 tập 1
Các mũi tên chỉ đường trong khu tham quan vườn thú ( Hình 1 ) gợi nên hình ảnh các vectơ trong không gian.
Vectơ trong không gian là gì? Các phép toán về vectơ trong không gian được thực hiện như thế nào?
Hoạt động 1 trang 56 SGK Toán 12 tập 1
Trong mặt phẳng, hãy nêu định nghĩa:
a) Vectơ, giá và độ dài của vectơ, hai vectơ cùng phương, hai vectơ cùng hướng;
b) Vectơ-không;
c) Hai vectơ bằng nhau, hai vectơ đối nhau.
Xem lời giải Toán 12 trang 56
Giải Toán 12 trang 57 Cánh diều
Luyện tập 1 trang 57 SGK Toán 12 tập 1
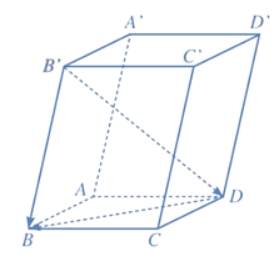
Cho hình hộp ABCD.A'B'C'D'. Hãy chỉ ra ba vectơ có điểm đầu và điểm cuối là các đỉnh của hình hộp sao cho mỗi vectơ đó:
a) Bằng vectơ 
\(\overrightarrow {AA'}\);
b) Là vectơ đối của vectơ −\(\overrightarrow {AA'}\).
Xem lời giải Toán 12 trang 57
Giải Toán 12 trang 58 Cánh diều
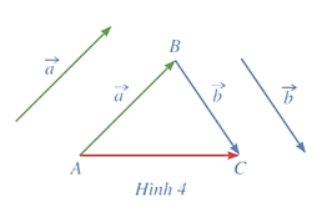
Hoạt động 2 trang 58 SGK Toán 12 tập 1
Trong không gian, cho 2 vec tơ \(\vec avà \vec b\). Lấy một điểm A tùy ý.
a) Vẽ \(\overrightarrow {AB} = \vec a,\overrightarrow {BC} = \vec b\)
b) Tổng của 2 vec tơ \(\vec a\) và \(\vec b\) bằng vec tơ nào trong hình 4?
Luyện tập 2 trang 58 SGK Toán 12 tập 1
Cho tứ diện ABCD. Chứng minh rằng: \(\overrightarrow {AC} + \overrightarrow {DB} = \overrightarrow {AB} + \overrightarrow {DC}\)
Xem lời giải Toán 12 trang 58
Giải Toán 12 trang 59 Cánh diều
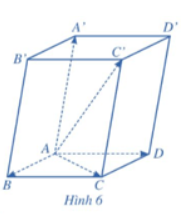
Hoạt động 3 trang 59 SGK Toán 12 tập 1
Cho hình hộp ABCD.A’B’C’D’. Tìm liên hệ giữa \(\overrightarrow {AB} + \overrightarrow {AD}\) và \(\overrightarrow {AC} ;\;\overrightarrow {AC} + \overrightarrow {AA'}\) và \(\overrightarrow {AC'}\)
Từ đó, hãy suy ra rằng
\(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AC'}\)
Luyện tập 3 trang 59 SGK Toán 12 tập 1
Cho hình hộp ABCD.A'B'C'D'. Chứng minh rằng: \(\overrightarrow {B'B}+\overrightarrow {AD}+\overrightarrow {CD}=\overrightarrow {B'D}\)
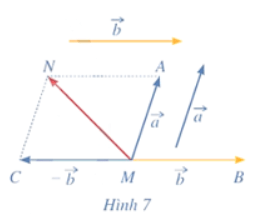
Hoạt động 4 trang 59 SGK Toán 12 tập 1
Trong không gian , cho hai vecto \(\;\vec a,\vec b.\;\) Lấy một điểm M tùy ý
a) Vẽ \(\overrightarrow {MA} = \vec a,\;\overrightarrow {MB} = \vec b\;,\overrightarrow {MC} = \overrightarrow { - b}\)
b) Tổng của hai vecto \(\vec a\;\) và \(\;\overrightarrow { - b}\) bằng vecto nào trong hình 7
Luyện tập 4 trang 59 SGK Toán 12 tập 1
Cho hình hộp ABCD.A'B'C'D'. Chứng minh rằng: \(\overrightarrow {BB'}-\overrightarrow {C'B'}-\overrightarrow {D'C'}=\overrightarrow {BD'}\)
Xem lời giải Toán 12 trang 59
Giải Toán 12 trang 60 Cánh diều
Hoạt động 5 trang 60 SGK Toán 12 tập 1
Nêu định nghĩa tích của một số thực \(k \ne 0\;\) với vecto \(\;\vec a\; \ne \vec 0\) trong mặt phẳng
Luyện tập 5 trang 60 SGK Toán 12 tập 1
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AD và BC, I là trung điểm MN. Chứng minh rằng:
a) \(\overrightarrow {MN}= \frac{1}{2} (\overrightarrow {AB}+\overrightarrow {DC})\)
b) \(\overrightarrow {IA}+\overrightarrow {IB}+\overrightarrow {IC}+\overrightarrow {ID}=\overrightarrow {0}\)
Xem lời giải Toán 12 trang 60
Giải Toán 12 trang 61 Cánh diều
Hoạt động 6 trang 61 SGK Toán 12 tập 1
Trong không gian, cho hai vecto \(\vec a,\vec b\) khác \(\;\vec 0\). Lấy một điểm O tùy ý.
a, Vẽ hai vecto \(\overrightarrow {OA} = \vec a,\;\overrightarrow {OB} = \vec b\)
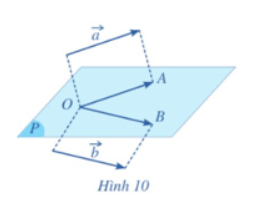
b, Khi đó , hai vecto \(\overrightarrow {OA} ,\overrightarrow {OB}\) có giá nằm trong cùng mặt phẳng (P) (hình 10). Nếu định nghĩa góc giữa hai vecto \(\overrightarrow {OA} ,\;\overrightarrow {OB}\) trong hai mặt phẳng (P)
Luyện tập 6 trang 61 SGK Toán 12 tập 1
Cho tứ diện đều ABCD. Gọi M, N lần lượt là trung điểm các cạnh AB, AC. Hãy tính góc giữa hai vectơ \(\overrightarrow {MN}, \overrightarrow {BD}\)
Hoạt động 7 trang 61 SGK Toán 12 tập 1
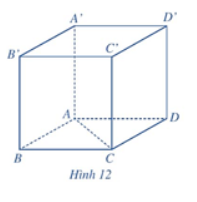
Trong không gian , cho hình lập phương ABCD.A’B’C’D’ có độ dài bằng 3cm (hình 12)
a, Tính góc giữa hai vecto \(\overrightarrow {AC} ,\overrightarrow {A'D'}\)
b, Tính \(\left| {\overrightarrow {AC} } \right|,\left| {\overrightarrow {A'D'} } \right|. Cos(\overrightarrow {AC} ,\overrightarrow {A'D'}\)
Xem lời giải Toán 12 trang 61
Giải Toán 12 trang 62 Cánh diều
Luyện tập 7 trang 62 SGK Toán 12 tập 1
ho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Tính \(\overrightarrow {A'B}.\overrightarrow {D'C'}, \overrightarrow {D'A}.\overrightarrow {BC}\)
Xem lời giải Toán 12 trang 62
Giải Toán 12 trang 63 Cánh diều
Bài 1 trang 63 SGK Toán 12 tập 1
Cho hình hộp ABCD. A’B’C’D’. Vecto \(\vec u = \overrightarrow {AA'} + \overrightarrow {A'B'} + \overrightarrow {A'D'}\) bằng vecto nào dưới đây?
a. \(\overrightarrow {A'C\;}\)
b. \(\overrightarrow {CA'}\)
c. \(\overrightarrow {AC'}\)
d. \(\overrightarrow {C'A}\)
Bài 2 trang 63 SGK Toán 12 tập 1
Cho tứ diện ABCD. Chứng minh rằng:
a, \(\overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {AD} + \overrightarrow {BC}\)
b, \(\overrightarrow {AB} - \overrightarrow {CD} = \overrightarrow {AC} + \overrightarrow {DB}\)
Bài 3 trang 63 SGK Toán 12 tập 1
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Tính
a. \(\overrightarrow {A'B} .\overrightarrow {D'C} ;\overrightarrow {D'A} .\overrightarrow {BC}\)
b. Các góc \(\left( {\overrightarrow {A'D} ,\overrightarrow {B'C'} } \right);\left( {\overrightarrow {AD',} \overrightarrow {BD} } \right)\)
Xem lời giải Toán 12 trang 63
Giải Toán 12 trang 64 Cánh diều
Bài 4 trang 64 SGK Toán 12 tập 1
Cho hình hộp ABCD.A’B’C’D’. Gọi G là trọng tâm tam giác AB’D’.Chứng minh rằng \(\overrightarrow {A'C} = 3\overrightarrow {A'G}\)
Bài 5 trang 64 SGK Toán 12 tập 1
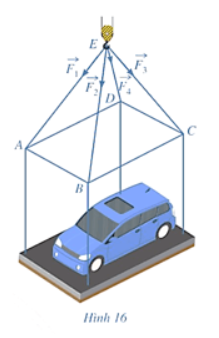
Một chiếc oto được đặt trên mặt đáy dưới của một khung sắt có dạng hình hộp chữ nhật với đáy trên là hinhg chữ nhật ABCD, mặt phẳng (ABCD) song song với mặt phẳng nằm ngang . Khung sắt có được buộc vào móc E của chiếc cần cẩu sao cho các đoạn dây cáp EA, EB, EC, ED có độ dài bằng nhau và cùng tạo với mặt phẳng (ABCD) một góc bằng \(60^\circ\)( hình 16 ). Chiếc cần cẩu kéo khung sắt lên theo phương thẳng đứng. Tính trọng lượng của chiếc xe oto ( làm tròn đến hàng đơn vị), biết rằng các lực căng \(\overrightarrow {{F_1},} \overrightarrow {{F_2},} \overrightarrow {{F_3},} \overrightarrow {{F_4}}\) đều có cường độ là 4700N và trọng lượng của khung sắt là 3000N.
Xem lời giải Toán 12 trang 64
Bài tiếp theo: Toán 12 Cánh diều bài 2: Toạ độ của vectơ
