Giải Toán 12 trang 53 tập 1 Kết nối tri thức
Giải Toán 12 trang 53 Tập 1
Giải Toán 12 trang 53 Tập 1 Kết nối tri thức hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 12 Kết nối tri thức tập 1 trang 53.
Câu hỏi trang 53 SGK Toán 12 tập 1 Kết nối
Hai vectơ 
\(1\vec{a}\) và \(\vec{a}\) có bằng nhau không? Hai vectơ \((-1)\vec{a}\) và \(-\vec{a}\) có bằng nhau không?
Hướng dẫn giải:
Ta có: \(1\vec{a} =\vec{a}\)
\((-1)\vec{a} =-\vec{a}\)
Luyện tập 7 trang 53 SGK Toán 12 tập 1 Kết nối
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi E, F lần lượt là các điểm thuộc cạnh SA, SB sao cho \(SE=\frac{1}{3}SA;\ SF=\frac{1}{3}SB\). Chứng minh rằng \(\overrightarrow {EF} =\frac{1}{3} \overrightarrow{DC}\).
Hướng dẫn giải:
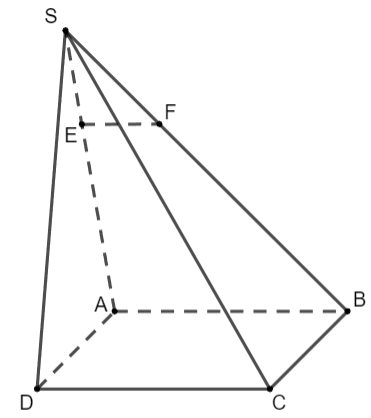
Xét tam giác SAB có \(\frac{SE}{SA}=\frac{SF}{SB}=\frac{1}{3}\)
⇒ EF // AB và \(EF=\frac{1}{3}AB\) (định lí Thales)
Vì ABCD là hình bình hành nên AB // DC và AB = DC
⇒ EF // DC và \(EF=\frac{1}{3}DC\)
Hai vectơ \(\overrightarrow {EF}\) và \(\overrightarrow{DC}\) cùng hướng nên \(\overrightarrow {EF} =\frac{1}{3} \overrightarrow{DC}\).
-----------------------------------------------
---> Bài tiếp theo: Giải Toán 12 trang 54 tập 1 Kết nối tri thức
Lời giải Toán 12 trang 53 Tập 1 Kết nối tri thức với các câu hỏi nằm trong Bài 6: Vectơ trong không gian, được VnDoc biên soạn và đăng tải!
