Giải Toán 12 trang 28 tập 1 Chân trời sáng tạo
Giải Toán 12 trang 28 Tập 1
Giải Toán 12 trang 28 Tập 1 hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 12 Chân trời sáng tạo tập 1 trang 28.
Thực hành 1 trang 28 SGK Toán 12 tập 1 Chân trời
Khảo sát và vẽ đồ thị của các hàm số sau:
a) y = – 2x3 – 3x2 + 1;
b) y = x3 + 3x2 + 3x + 2.
Hướng dẫn giải:
a) Xét hàm số: y = – 2x3 – 3x2 + 1
1. Tập xác định: 
\(\mathbb{R}\).
2. Sự biến thiên:
- Chiều biến thiên:
Đạo hàm y' = - 6x2 - 6x;
y' = 0 ⇔ x = 0 hoặc x = - 1.
Trên các khoảng \((– ∞; – 1)\) và \((0; + ∞)\), y' < 0 nên hàm số nghịch biến trên mỗi khoảng đó.
Trên khoảng \((– 1; 0)\), y' > 0 nên hàm số đồng biến trên khoảng đó.
- Cực trị:
Hàm số đạt cực đại tại x = 0 và yCĐ = 1.
Hàm số đạt cực tiểu tại x = – 1 và yCT = 0.
- Các giới hạn tại vô cực:
\(\lim_{x \rightarrow -\infty} y=\lim_{x \rightarrow -\infty}x^3 \left ( -2-\frac{3}{x }+\frac{ 1}{x^3} \right ) =+∞\)
\(\lim_{x \rightarrow +\infty} y=\lim_{x \rightarrow +\infty}x^3 \left ( -2-\frac{3}{x }+\frac{ 1}{x^3} \right ) =-∞\)
- Bảng biến thiên:
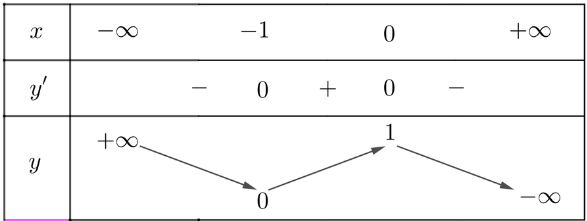
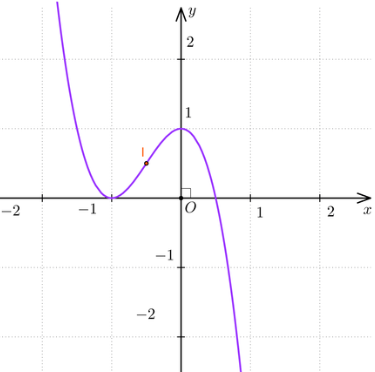
3. Đồ thị
Khi x = 0 thì y = 1 nên (0; 1) là giao điểm của đồ thị với trục Oy.
Ta có y = 0 ⇔ – 2x3 – 3x2 + 1 = 0
⇔ x = - 1 hoặc \(x=\frac{1}{2}\).
Vậy đồ thị của hàm số giao với trục Ox tại hai điểm (- 1; 0) và \(\left(\frac{1}{2};0\right)\).
Điểm (0; 1) là điểm cực đại và điểm (- 1; 0) là điểm cực tiểu của đồ thị hàm số.
Đồ thị của hàm số có tâm đối xứng là điểm \(I\left(-\frac{1}{2};\frac{1}{2}\right)\).
b) y = x3 + 3x2 + 3x + 2.
1. Tập xác định: \(\mathbb{R}\).
2. Sự biến thiên:
- Chiều biến thiên:
Đạo hàm y' = 3x2 + 6x + 3
y' = 0 ⇔ x = - 1.
Trên khoảng \((– \infty ; + \infty )\), y' ≥ 0 nên hàm số đồng biến trên khoảng đó.
- Cực trị: Hàm số không có cực trị.
- Các giới hạn tại vô cực:
\(\lim_{x \rightarrow -\infty} y=\lim_{x \rightarrow -\infty}x^3 \left ( 1 +\frac{3}{x }+\frac{3}{x^2 }+\frac{ 2}{x^3} \right ) =-∞\)
\(\lim_{x \rightarrow +\infty} y=\lim_{x \rightarrow +\infty}x^3 \left ( 1 +\frac{3}{x }+\frac{3}{x^2 }+\frac{ 2}{x^3} \right ) =+∞\)
- Bảng biến thiên:
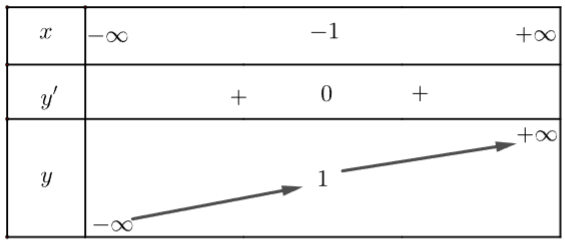
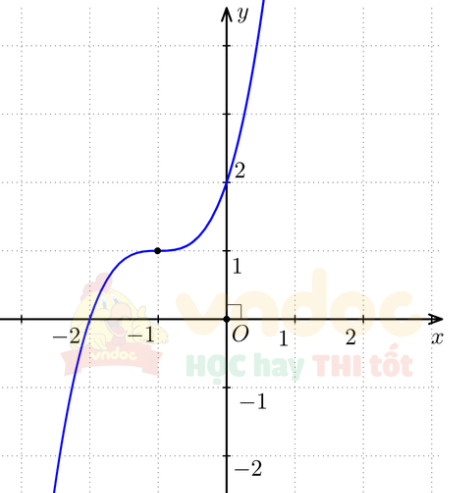
3. Đồ thị
Khi x = 0 thì y = 2 nên (0; 2) là giao điểm của đồ thị với trục Oy.
Ta có y = 0 ⇔ x3 + 3x2 + 3x + 2 = 0
⇔ x = - 2.
Vậy đồ thị của hàm số giao với trục Ox tại điểm (- 2; 0).
Đồ thị của hàm số có tâm đối xứng là điểm I(- 1; 1).
-----------------------------------------------
---> Xem thêm: Giải Toán 12 trang 30 tập 1 Chân trời sáng tạo
Lời giải Toán 12 trang 28 Tập 1 Chân trời sáng tạo với các câu hỏi nằm trong Bài 4: Khảo sát và vẽ đồ thị một số hàm số cơ bản, được VnDoc biên soạn và đăng tải!
