VnDoc.com

Toán 12 Cánh diều bài tập cuối chương 2

Bài trước

Bài sau

Giải bài tập Toán 12 CD bài tập cuối chương 2

Giải Toán 12 trang 82 Cánh diều
Giải Toán 12 trang 83 Cánh diều

Toán 12 Cánh diều bài tập cuối chương 2 được VnDoc.com tổng hợp gồm hướng dẫn giải SGK Toán 12 Cánh diều tập 1 các trang 82, 83. Mời các bạn cùng theo dõi bài viết dưới đây nhé.

Giải Toán 12 trang 82 Cánh diều

Bài 1 trang 82 SGK Toán 12 tập 1

Cho điểm M thỏa mãn $\overrightarrow {OM} = 3\overrightarrow i + 4\overrightarrow j + 2\overrightarrow k$ $\overrightarrow {OM} = 3\overrightarrow i + 4\overrightarrow j + 2\overrightarrow k$. Tọa độ của điểm M là:

A. (2;3;4)

B. (3;4;2)

C. (4,2,3)

D. (3;2;4)

Bài 2 trang 82 SGK Toán 12 tập 1

Cho hai điểm M(1; – 2; 3) và N(3; 4; – 5). Tọa độ của vectơ $\overrightarrow {NM}$ $\overrightarrow {NM}$ là:

A. (– 2; 6; 8).

B. (2; 6; – 8).

C. (– 2; 6; – 8).

D. (– 2; – 6; 8).

Bài 3 trang 82 SGK Toán 12 tập 1

Cho hai vectơ $\overrightarrow {u}$ $\overrightarrow {u}$ = (3;−4;5), $\overrightarrow {v}$ $\overrightarrow {v}$ = (5;7;−1). Tọa độ của vectơ $\overrightarrow {u} + \overrightarrow {v}$ $\overrightarrow {u} + \overrightarrow {v}$ là:

A. (8; 3; 4).

B. (– 2; – 11; 6).

C. (2; 11; – 6).

D. (– 8; – 3; – 4).

Bài 4 trang 82 SGK Toán 12 tập 1

Cho hai vectơ $\overrightarrow {u}$ $\overrightarrow {u}$ = (1;–2;3), $\overrightarrow {v}$ $\overrightarrow {v}$ = (5;4;−1). Tọa độ của vectơ $\overrightarrow {u} - \overrightarrow {v}$ $\overrightarrow {u} - \overrightarrow {v}$ là:

A. (4; 6; 4).

B. (– 4; – 6; 4).

C. (4; 6; – 4).

D. (– 4; – 6; – 4).

Bài 5 trang 82 SGK Toán 12 tập 1

Cho vectơ $\overrightarrow {u}$ $\overrightarrow {u}$ = (1;−1;3). Tọa độ của vectơ −3 $\overrightarrow {u}$ $\overrightarrow {u}$ là:

A. (3; – 3; 9).

B. (3; – 3; – 9).

C. (– 3; 3; – 9).

D. (3; 3; 9).

Bài 6 trang 82 SGK Toán 12 tập 1

Độ dài của vectơ $\overrightarrow {u}$ $\overrightarrow {u}$ = (2;−2;1) là:

A. 9.

B. 3.

C. 2.

D. 4.

Bài 7 trang 82 SGK Toán 12 tập 1

Tích vô hướng của hai vecto $\overrightarrow u = (1; - 2;3),\overrightarrow v = (3;4; - 5)$ $\overrightarrow u = (1; - 2;3),\overrightarrow v = (3;4; - 5)$ là:

A. $\sqrt {14} .\sqrt {50}$ $\sqrt {14} .\sqrt {50}$

B. $- \sqrt {14} .\sqrt {50}$ $- \sqrt {14} .\sqrt {50}$

C. 20

D. -20

Bài 8 trang 82 SGK Toán 12 tập 1

Khoảng cách giữa hai điểm I(1; 4; – 7) và K(6; 4; 5) là:

A. 169.

B. 13.

C. 26.

D. 6,5.

Bài 9 trang 82 SGK Toán 12 tập 1

Cho hai điểm M(1; – 2; 3) và N(3; 4; – 5). Trung điểm của đoạn thẳng MN có tọa độ là:

A. (– 2; 1; 1).

B. (2; 1; 1).

C. (– 2; 1; – 1).

D. (2; 1; – 1).

Bài 10 trang 82 SGK Toán 12 tập 1

Cho tam giác MNP có M(0; 2; 1), N(–1; –2; 3) và P(1; 3; 2). Trọng tâm của tam giác MNP có tọa độ là:

A. (0; 1; 2).

B. (0; 3; 6).

C. (0; – 3; – 6).

D. (0; – 1; – 2).

Xem lời giải Toán 12 trang 82

Giải Toán 12 trang 83 Cánh diều

Bài 11 trang 83 SGK Toán 12 tập 1

Cho hai vectơ $\overrightarrow {u}$ $\overrightarrow {u}$ = (1;−2;3) và $\overrightarrow {v}$ $\overrightarrow {v}$ = (3;4;−5). Hãy chỉ ra tọa độ của một vectơ $\overrightarrow {w}$ $\overrightarrow {w}$ khác $\overrightarrow {0}$ $\overrightarrow {0}$ vuông góc với cả hai vectơ $\overrightarrow {u}$ $\overrightarrow {u}$ và $\overrightarrow {v}$ $\overrightarrow {v}$.

Bài 12 trang 83 SGK Toán 12 tập 1

ho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AA' và CC'. Tính góc giữa hai vectơ $\overrightarrow {MN}$ $\overrightarrow {MN}$ và $\overrightarrow {AD$ $\overrightarrow {AD'}$.

Bài 13 trang 83 SGK Toán 12 tập 1

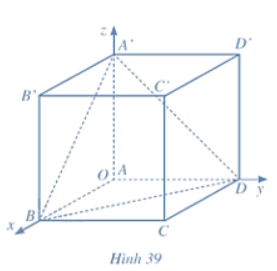
Xét hệ toạ độ Oxyz gắn với hình lập phương ABCD.A'B'C'D' như Hình 39, đơn vị của mỗi trục bằng độ dài cạnh hình lập phương. Biết A(0; 0; 0), B(1; 0; 0), D(0; 1; 0), A'(0; 0; 1).

a) Xác định toạ độ các đỉnh còn lại của hình lập phương ABCD.A'B'C'D'.

b) Xác định toạ độ trọng tâm G của tam giác A'BD.

c) Xác định toạ độ các vectơ $\overrightarrow {OG}$ $\overrightarrow {OG}$ và $\overrightarrow {OC$ $\overrightarrow {OC'}$. Chứng minh rằng ba điểm O, G, C' thẳng hàng và OG = $\frac{1}{3} \overrightarrow {OC$ $\frac{1}{3} \overrightarrow {OC'}$.

Giải Toán 12 trang 83 Cánh diều

Bài 14 trang 83 SGK Toán 12 tập 1

Trong không gian với hệ toạ độ Oxyz, cho A(2; 0; – 3), B(0; – 4; 5) và C(– 1; 2; 0).

a) Chứng minh rằng ba điểm A, B, C không thẳng hàng.

b) Tìm toạ độ của điểm D sao cho tứ giác ABCD là hình bình hành.

c) Tìm toạ độ trọng tâm G của tam giác ABC.

d) Tính chu vi của tam giác ABC.

e) Tính $\hat{BAC}$ $\hat{BAC}$

Bài 15 trang 83 SGK Toán 12 tập 1

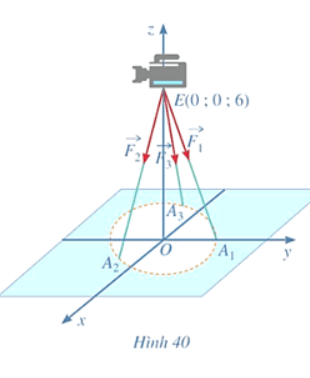
Một chiếc máy được đặt trên một giá đỡ ba chân với điểm đặt E(0;0;6) và các điểm tiếp xúc với mặt đất của ba chân lần lượt là ${A_1}(0;1;0), {A_2}(\frac{{\sqrt 3 }}{2}; - \frac{1}{2};0), {A_3}( - \frac{{\sqrt 3 }}{2}; - \frac{1}{2};0)$ ${A_1}(0;1;0), {A_2}(\frac{{\sqrt 3 }}{2}; - \frac{1}{2};0), {A_3}( - \frac{{\sqrt 3 }}{2}; - \frac{1}{2};0)$ (Hình 40). Biết rằng trọng lượng của chiếc máy là 300N. Tìm tọa độ của các lực tác dụng lên giá đỡ $\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,\overrightarrow {{F_3}}$ $\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,\overrightarrow {{F_3}}$

Giải Toán 12 trang 83 Cánh diều