Giải Toán 12 trang 72 tập 1 Chân trời sáng tạo

Giải Toán 12 trang 72 Tập 1

Thực hành 2 trang 72 SGK Toán 12 tập 1 Chân trời

Giải Toán 12 trang 72 Tập 1 hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 12 Chân trời sáng tạo tập 1 trang 72.

Thực hành 2 trang 72 SGK Toán 12 tập 1 Chân trời

Hãy so sánh khoảng tứ phân vị của mẫu số liệu ghép nhóm về thời gian tập thể dục buổi sáng mỗi ngày của bác Bình và bác An trong Hoạt động khởi động.

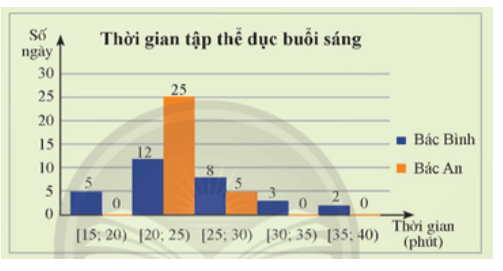
Hoạt động: Biểu đồ dưới đây thống kê thời gian tập thể dục buổi sáng mỗi ngày trong tháng 9/2022 của bác Bình và bác An.

Ai là người có thời gian tập đều hơn?

Giải Toán 12 trang 68 Chân trời

Hướng dẫn giải:

Xét mẫu số liệu ghép nhóm về thời gian tập thể dục buổi sáng mỗi ngày của bác Bình

Cỡ mẫu: n = 30

Giả sử x₁, x₂, …, x₃₀ là mẫu số liệu gốc gồm thời gian tập thể dục mỗi ngày của bác Bình được sắp xếp theo thứ tự không giảm.

Ta có: x₁, x₂, …, x₅ ∈ [15; 20); x₆, x₇, …, x₁₇ ∈ [20; 25); x₁₈, x₁₉, …, x₂₅ ∈ [25; 30);

x₂₆, x₂₇, x₂₈ ∈ [30; 35); x₂₉, x₃₀∈ [35; 40);

Tứ phân vị thứ nhất của mẫu số liệu gốc là x₈ ∈ [20; 25). Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:

$Q_1=20+\frac{\frac{30}{4}-5}{12}.\left(25-20\right)= \frac{505}{24}$

Tứ phân vị thứ ba của mẫu số liệu gốc là x₂₃ ∈ [25; 30). Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:

$Q_3=25+\frac{\frac{3.30}{4}-(5+12)}{8}.\left(30-25\right)=\frac{455}{16}$

Vậy khoảng tứ phân vị của mẫu số liệu ghép nhóm về thời gian tập thể dục buổi sáng mỗi ngày của bác Bình là: $\triangle _Q=\frac{455}{16}-\frac{505}{24} =\frac{355}{48}$

Xét mẫu số liệu ghép nhóm về thời gian tập thể dục buổi sáng mỗi ngày của bác An

Cỡ mẫu: n = 30

Giả sử x₁, x₂, …, x₃₀ là mẫu số liệu gốc gồm thời gian tập thể dục mỗi ngày của bác Bình được sắp xếp theo thứ tự không giảm.

Ta có: x₁, x₂, …, x₂₅ ∈ [20; 25); x₂₆, x₂₇, …, x₃₀ ∈ [25; 30)

Tứ phân vị thứ nhất của mẫu số liệu gốc là x₈ ∈ [20; 25). Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:

$Q_1=20+\frac{\frac{30}{4}-0}{25}.\left(25-20\right)= \frac{43}{2}$

Tứ phân vị thứ ba của mẫu số liệu gốc là x₂₃ ∈ [20; 25). Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:

$Q_3=20+\frac{\frac{3.30}{4}-0}{25}.\left(25-20\right)=\frac{49}{2}$

Vậy khoảng tứ phân vị của mẫu số liệu ghép nhóm về thời gian tập thể dục buổi sáng mỗi ngày của bác An là: $\triangle _Q=\frac{49}{2}-\frac{43}{2} =3$

Do $\frac{355}{48}>3$ nên khoảng tứ phân vị của mẫu số liệu ghép nhóm về thời gian tập thể dục buổi sáng mỗi ngày của bác Bình lớn hơn khoảng tứ phân vị của mẫu số liệu ghép nhóm về thời gian tập thể dục buổi sáng mỗi ngày của bác An.

-----------------------------------------------

---> Xem thêm: Giải Toán 12 trang 73 tập 1 Chân trời sáng tạo

Lời giải Toán 12 trang 72 Tập 1 Chân trời sáng tạo với các câu hỏi nằm trong Bài 1: Khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu ghép nhóm, được VnDoc biên soạn và đăng tải!

Chia sẻ, đánh giá bài viết

1

Bài trước

Bài sau