Giải Toán 12 trang 47 tập 1 Chân trời sáng tạo
Giải Toán 12 trang 47 Tập 1
Giải Toán 12 trang 47 Tập 1 hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 12 Chân trời sáng tạo tập 1 trang 47.
Thực hành 6 trang 47 SGK Toán 12 tập 1 Chân trời
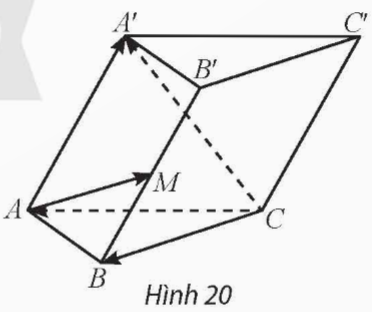
Cho hình lăng trụ ABC.A'B'C' có M là trung điểm của BB' (Hình 20). Đặt 
\(\overrightarrow{CA}=\overrightarrow{a};\ \overrightarrow{CB}=\overrightarrow{b};\ \overrightarrow{CC'}=\overrightarrow{c}\). Chứng minh rằng \(\overrightarrow{AM}=\overrightarrow{b}-\overrightarrow{a}+\frac{1}{2}\overrightarrow{c\ }\).
Hướng dẫn giải:
Ta có: \(\overrightarrow{AM}=\overrightarrow{CM}-\overrightarrow{CA}\)
\(=\frac{1}{2}\overrightarrow{CB}+\frac{1}{2}\overrightarrow{CB'}-\overrightarrow{CA}\)
\(=\frac{1}{2}\overrightarrow{CB}+\frac{1}{2}\left(\overrightarrow{CB}+\overrightarrow{CC'}\right)-\overrightarrow{CA}\)
\(=\frac{1}{2}\overrightarrow{CB}+\frac{1}{2}\overrightarrow{CB}+\frac{1}{2}\overrightarrow{CC'}-\overrightarrow{CA}\)
\(=\overrightarrow{CB}-\overrightarrow{CA}+\frac{1}{2}\overrightarrow{CC'}\)
Vậy \(\overrightarrow{AM}=\overrightarrow{b}-\overrightarrow{a}+\frac{1}{2}\overrightarrow{c\ }\).
-----------------------------------------------
---> Xem thêm: Giải Toán 12 trang 48 tập 1 Chân trời sáng tạo
Lời giải Toán 12 trang 47 Tập 1 Chân trời sáng tạo với các câu hỏi nằm trong Bài 1: Vectơ và các phép toán trong không gian, được VnDoc biên soạn và đăng tải!
