Giải Toán 12 trang 7 tập 1 Kết nối tri thức

Giải Toán 12 trang 7 Tập 1 Kết nối tri thức hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 12 Kết nối tri thức tập 1 trang 7.

Hoạt động 2 trang 7 SGK Toán 12 tập 1 KNTT

Xét hàm số \(y=\left\{ \begin{array}{l} - x \ \ nếu \ \ x < - 1 \\ 1 \ \ nếu \ - 1\le x \le 1 \\ x \ \ nếu \ \ x > 1\end{array} \right.\) có đồ thị như Hình 1.6.

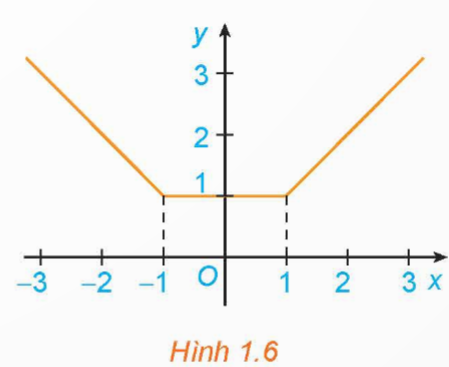
a) Xét dấu đạo hàm của hàm số trên các khoảng (- ∞; - 1), (1; + ∞). Nêu nhận xét về mối quan hệ giữa tính đồng biến, nghịch biến và dấu đạo hàm của hàm số trên mỗi khoảng này.

b) Có nhận xét gì về đạo hàm y' và hàm số y trên khoảng (- 1; 1)?

Hướng dẫn giải:

a) Xét khoảng (- ∞; - 1):

Ta có hàm số: y = - x

y' = - 1

Vậy trong khoảng (- ∞; - 1), hàm số nghịch biến và y' < 0

Xét khoảng (1; + ∞):

Ta có hàm số: y = x

y' = 1

Vậy trong khoảng (1; + ∞), hàm số đồng biến và y' > 0

b) Xét khoảng (- 1; 1):

Ta có hàm số: y = 1

y' = 0

Vậy trong khoảng (- 1; 1), hàm số không đổi và y' = 0

Luyện tập 2 trang 7 SGK Toán 12 tập 1 KNTT

Tìm các khoảng đồng biến, khoảng nghịch biến của hàm số y = - x² + 2x + 3.

Hướng dẫn giải:

Tập xác định của hàm số là R.

Ta có: y' = - 2x + 2;

y ' > 0 với x ∈ (- ∞; 1); y' < 0 với x ∈ (1; + ∞).

Do đó, hàm số đồng biến trên khoảng (- ∞; 1) và nghịch biến trên khoảng (1; + ∞).

Hoạt động 3 trang 7 SGK Toán 12 tập 1 KNTT

Cho hàm số y = f(x) = x³ - 3x² + 2x + 1.

a) Tính đạo hàm f'(x) và tìm các điểm x mà f'(x) = 0.

b) Lập bảng biến thiên của hàm số, tức là lập bảng thể hiện dấu của đạo hàm và sự đồng biến, nghịch biến của hàm số trên các khoảng tương ứng.

c) Nếu kết luận về khoảng đồng biến, nghịch biến của hàm số.

Hướng dẫn giải:

a) Ta có: y' = 3x² - 6x + 2

Cho y' = 0 thì 3x² - 6x + 2 = 0 \(\Leftrightarrow \left[ \begin{array}{l}x = \frac{3+\sqrt{3} }{3} \\x = \frac{3-\sqrt{3} }{3}\end{array} \right.\)

b) Ta có bảng biến thiên như sau:

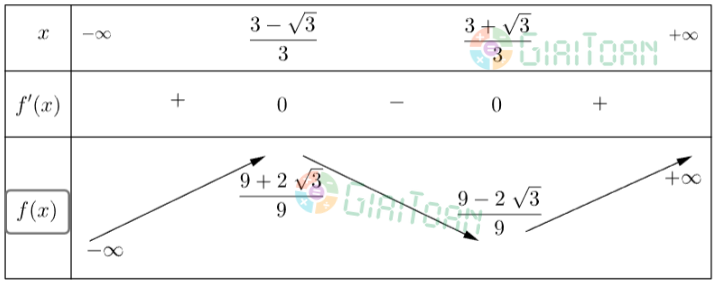
c) Hàm số đồng biến trên khoảng \(\left(-∞;\frac{3-\sqrt{3}}{3}\right)\) và \(\left(\frac{3+\sqrt{3}}{3};+∞\right)\)

Hàm số nghịch biến trên khoảng \(\left(\frac{3-\sqrt{3}}{3};\frac{3+\sqrt{3}}{3}\right)\)

-----------------------------------------------

---> Xem thêm: Giải Toán 12 trang 9 tập 1 Kết nối tri thức

Lời giải Toán 12 trang 7 Tập 1 Kết nối tri thức với các câu hỏi nằm trong Bài 1 Tính đơn điệu và cực trị của hàm số, được VnDoc biên soạn và đăng tải!