Giải Toán 12 trang 53 tập 1 Chân trời sáng tạo
Giải Toán 12 trang 53 Tập 1
Giải Toán 12 trang 53 Tập 1 hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 12 Chân trời sáng tạo tập 1 trang 53.
Thực hành 1 trang 53 SGK Toán 12 tập 1 Chân trời
Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng 1, SA vuông góc với mặt phẳng đáy và có độ dài bằng 1 (Hình 4). Vẽ hệ trục toạ độ Oxyz có gốc O trùng với điểm A, các điểm B, D, S lần lượt nằm trên các tia Ox, Oy, Oz và chỉ ra các vectơ đơn vị trên các trục toạ độ.
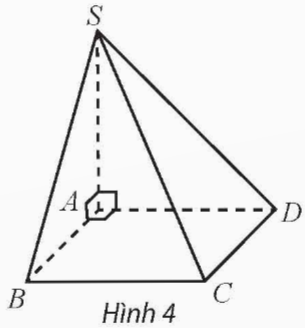
Hướng dẫn giải:
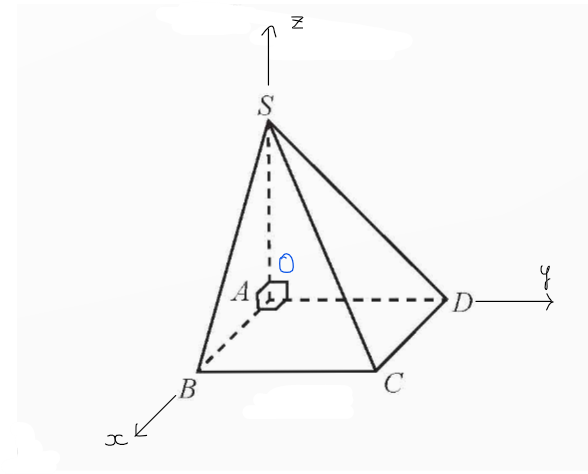
Các vectơ đơn vị trên ba trục tọa độ lần lượt là: 
\(\overrightarrow{AB};\ \overrightarrow{AD};\ \overrightarrow{AS}\).
Vận dụng 1 trang 53 SGK Toán 12 tập 1 Chân trời
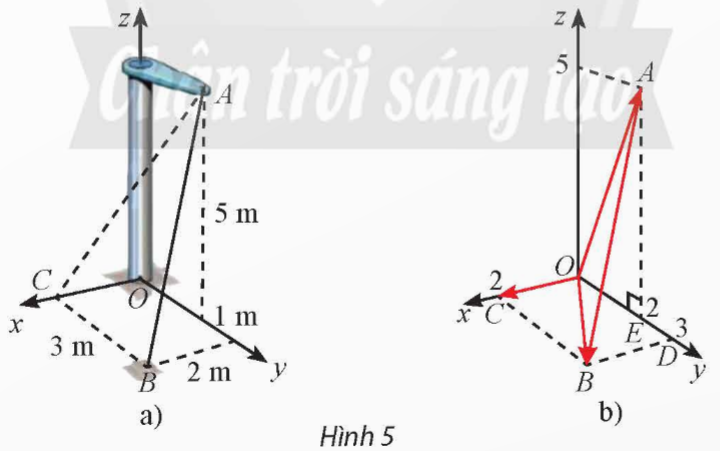
Một thiết kế cơ khí trong Hình 5a được biểu diễn trong không gian Oxyz như Hình 5b.
a) Hãy vẽ ba vectơ đơn vị \(\overrightarrow{i},\overrightarrow{j},\overrightarrow{k\ }\) lần lượt trên ba trục toạ độ Ox, Oy, Oz (mỗi vectơ đơn vị có độ dài bằng 1m).
b) Biểu diễn các vectơ \(\overrightarrow{OC},\overrightarrow{OB},\overrightarrow{OA}\) theo \(\overrightarrow{i},\overrightarrow{j},\overrightarrow{k\ }\).
Hướng dẫn giải:
a)
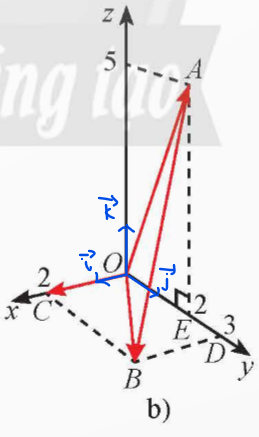
b) \(\overrightarrow{OC\ }=2\overrightarrow{i\ }\); \(\overrightarrow{OB\ }=2\overrightarrow{i\ }+3\overrightarrow{j\ \ }\); \(\overrightarrow{OA\ }=2\overrightarrow{j\ }+5\overrightarrow{k\ \ }\)
Hoạt động 2 trang 53 SGK Toán 12 tập 1 Chân trời
Cho hình hộp chữ nhật OABC.O′A′B′C′ có cạnh OA = 3, OC = 5, OO′ = 2. Vẽ ba vectơ đơn vị \(\overrightarrow{i},\overrightarrow{j},\overrightarrow{k\ }\) lần lượt trên các cạnh OA, OC, OO′. Biểu diễn \(\overrightarrow {OB'}\) theo ba vectơ \(\overrightarrow{i},\overrightarrow{j},\overrightarrow{k\ }\)
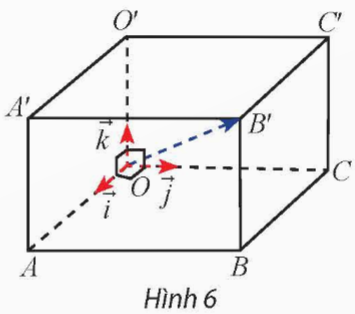
Hướng dẫn giải:
Áp dụng quy tắc hình hộp, ta có:
\(\overrightarrow{OB'}=\overrightarrow{OA}+\overrightarrow{OC}+\overrightarrow{OO'}=3\overrightarrow{i}+5\overrightarrow{j}+2\overrightarrow{k\ }\)
-----------------------------------------------
---> Xem thêm: Giải Toán 12 trang 54 tập 1 Chân trời sáng tạo
Lời giải Toán 12 trang 53 Tập 1 Chân trời sáng tạo với các câu hỏi nằm trong Bài 2: Toạ độ của vectơ trong không gian, được VnDoc biên soạn và đăng tải!
