Giải Toán 12 trang 16 tập 1 Cánh diều
Giải Toán 12 trang 16 Cánh diều Tập 1
Giải Toán 12 trang 16 Tập 1 hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 12 Cánh diều tập 1 trang 16.
Luyện tập 1 trang 16 SGK Toán 12 tập 1
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số 
\(f(x) = \sqrt{9-x^{2} }\) trên đoạn [– 3; 3]
Hướng dẫn giải:
Do 0 ≤ x2 ≤ 9 với mọi x ∈ [– 3; 3] nên 0 ≤ 9 – x2 ≤ 9 với mọi x ∈ [– 3; 3]
Suy ra 0 ≤ \(\sqrt{9-x^{2} }\) ≤ 3 với mọi x ∈ [– 3; 3]
Tức là 0 ≤ f(x) ≤ 3 với mọi x ∈ [– 3; 3].
Ta có f(0) = 3 nên \(\underset{[-3;3]}{\max} f(x) = 3\);
f(– 3) = f(3) = 0 nên \(\underset{[-3;3]}{\min} f(x) = 0\).
Hoạt động 2 trang 16 SGK Toán 12 tập 1
Cho hàm số \(f\left(x\right)=x+\frac{1}{x-1}\) với x > 1.
a) Tính \(\lim_{x \rightarrow 1 ^+} f(x), \ \lim_{x \rightarrow +\infty } f(x)\)
b) Lập bảng biến thiên của hàm số f(x) trên khoảng \((1;+\infty)\)
c) Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của hàm số f(x) trên khoảng \((1;+\infty)\)
Hướng dẫn giải:
a) \(\lim_{x \rightarrow 1 ^+} f(x) = \lim_{x \rightarrow 1 ^+} \left ( x+\frac{1}{x-1} \right ) =+\infty\)
\(\lim_{x \rightarrow +\infty } f(x) = \lim_{x \rightarrow +\infty } \left ( x+\frac{1}{x-1} \right ) =+\infty\)
b) Ta có: \(f'\left(x\right)=1-\frac{1}{\left(x-1\right)^2}\)
f'(x) = 0 ⇔ x = 2 (vì x > 1)
Bảng biến thiên của hàm số f(x):
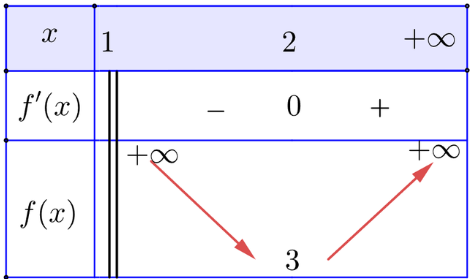
c) Từ bảng biến thiên ta có \(\underset{[1;+\infty ]}{\min} f(x) = 3\), hàm số không có giá trị lớn nhất.
Luyện tập 2 trang 16 SGK Toán 12 tập 1
Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của hàm số \(y = \frac{2x-5}{x-1}\) trên nửa khoảng (1; 3]
Hướng dẫn giải:
-----------------------------------------------
---> Xem thêm: Giải Toán 12 trang 17 tập 1 Cánh diều
Lời giải Toán 12 trang 16 Tập 1 Cánh diều với các câu hỏi nằm trong Bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số, được VnDoc biên soạn và đăng tải!
