Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm

VnDoc.com

Giải Toán 12 trang 12 tập 1 Chân trời sáng tạo

Bài trước

Tải về

Bài sau

Giải Toán 12 trang 12 Tập 1

Thực hành 5 trang 12 SGK Toán 12 tập 1 Chân trời
Vận dụng 2 trang 12 SGK Toán 12 tập 1 Chân trời

Giải Toán 12 trang 12 Tập 1 hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 12 Chân trời sáng tạo tập 1 trang 12.

Thực hành 5 trang 12 SGK Toán 12 tập 1 Chân trời

Tìm cực trị của hàm số $g(x) = \frac{x^{2}+x+4 }{x+1}$ $g (x) = \frac{x^{2} + x + 4}{x + 1}$ .

Hướng dẫn giải:

Tập xác định của hàm số là ℝ \ {- 1}.

Ta có: $y^{'} = \frac{x^{2} + 2 x - 3}{{(x + 1)}^{2}}$

y' = 0 $\Leftrightarrow$ $\Leftrightarrow$ x = 1 hoặc x = - 3

Lập bảng biến thiên của hàm số:

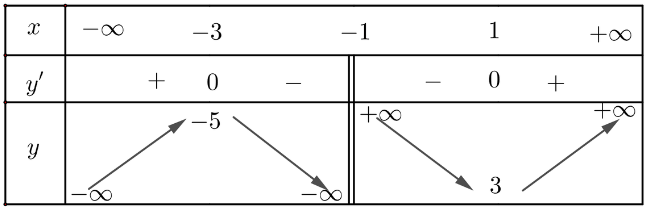
Vậy hàm số đạt cực đại tại x = - 3, giá trị cực đại là f(- 3) = - 5; hàm số đạt cực tiểu tại x = 1, giá trị cực tiểu là f(1) = 3.

Vận dụng 2 trang 12 SGK Toán 12 tập 1 Chân trời

Một phần lát cắt của dãy núi có độ cao tính bằng mét được mô tả bởi hàm số

$y= h (x)=−\frac{1}{1320000} x^{3} + \frac{9}{3520} x^{2}-\frac{81}{44} x+840$ $y = h (x) = - \frac{1}{1320000} x^{3} + \frac{9}{3520} x^{2} - \frac{81}{44} x + 840$ với 0 ≤ x ≤ 2 000.

Tìm tọa độ các đỉnh của lát cắt dãy núi trên đọan [0; 2000].

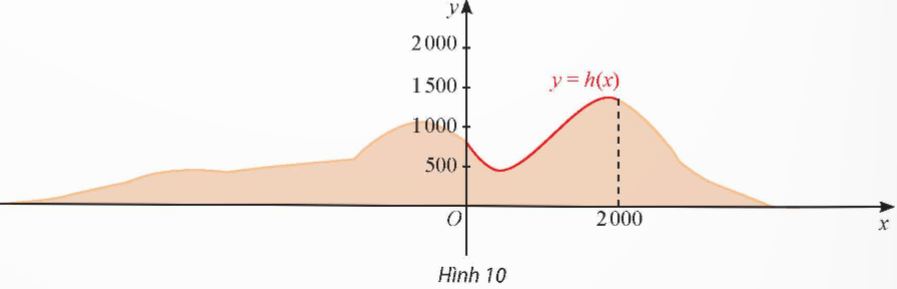
(Theo: Tập bản đồ bài tập và bài thực hành Địa lí 8, Nhà xuất bản Giáo dục Việt Nam, 2011).

Hướng dẫn giải:

Đang cập nhật...

-----------------------------------------------

---> Xem thêm: Giải Toán 12 trang 13 tập 1 Chân trời sáng tạo

Lời giải Toán 12 trang 12 Tập 1 Chân trời sáng tạo với các câu hỏi nằm trong Bài 1 Tính đơn điệu và cực trị của hàm số, được VnDoc biên soạn và đăng tải!

Xem thêm các bài Tìm bài trong mục này khác:

Chia sẻ, đánh giá bài viết

133

Bài trước

Bài sau

Chia sẻ bởi:
Milky Nugget

Đóng Chỉ thành viên VnDoc PRO/PROPLUS tải được nội dung này!

Đóng

79.000 / tháng

Mua ngay

Đặc quyền các gói Thành viên

PRO

Phổ biến nhất

PRO+

Tải tài liệu Cao cấp 1 Lớp

Tải tài liệu Trả phí + Miễn phí

Xem nội dung bài viết

Trải nghiệm Không quảng cáo

Làm bài trắc nghiệm không giới hạn

Tìm hiểu thêm

Mua cả năm Tiết kiệm tới 48%

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!