Toán 12 Chân trời sáng tạo bài tập cuối chương 2

Giải bài tập Toán 12 CTST bài tập cuối chương 2

Giải Toán 12 trang 65 Chân trời
Giải Toán 12 trang 66 Chân trời

Toán 12 Chân trời sáng tạo bài tập cuối chương 2 được VnDoc.com tổng hợp với hướng dẫn giải bài tập SGK Toán 12 Chân trời sáng tạo tập 1 các trang 65, 66.

Giải Toán 12 trang 65 Chân trời

Bài 1 trang 65 SGK Toán 12 tập 1

Cho điểm M thoả mãn $\overrightarrow {OM} = 2\overrightarrow i + \overrightarrow j$ $\overrightarrow {OM} = 2\overrightarrow i + \overrightarrow j$. Toạ độ của điểm M là

A. M(0; 2; 1).

B. M(1; 2; 0).

C. M(2; 0; 1).

D. M(2; 1; 0).

Bài 2 trang 65 SGK Toán 12 tập 1

Cho hai điểm A(–1; 2; –3) và B(2; –1; 0). Toạ độ của vectơ $\overrightarrow {AB}$ $\overrightarrow {AB}$ là

A. $\overrightarrow {AB}$ $\overrightarrow {AB}$ = (1; –1; 1).

B. $\overrightarrow {AB}$ $\overrightarrow {AB}$ = (3; 3; –3).

C. $\overrightarrow {AB}$ $\overrightarrow {AB}$ = (1; 1; –3).

D. $\overrightarrow {AB}$ $\overrightarrow {AB}$ = (3; –3; 3).

Bài 3 trang 65 SGK Toán 12 tập 1

Cho hai điểm A(3; −2; 3) và B(−1; 2; 5). Tọa độ trung điểm I của đoạn thẳng AB là

A. I(−2; 2; 1).

B. I(1; 0; 4).

C. I(2; 0; 8).

D. I(2; −2; −1).

Bài 4 trang 65 SGK Toán 12 tập 1

Cho ba điểm A(1; 3; 5), B(2; 0; 1), C(0; 9; 0). Tọa độ trọng tâm G của tam giác ABC là

A. G(3; 12; 6).

B. G(1; 5; 2).

C. G(1; 0; 5).

D. G(1; 4; 2).

Bài 5 trang 65 SGK Toán 12 tập 1

Cho A(1; 2; −1), B(2; 1; −3), C(−3; 5; 1). Điểm D sao cho ABCD là hình bình hành có tọa độ là

A. D(−4; 6; 3).

B. D(−2; 2; 5).

C. D(−2; 8; −3).

D. D(−4; 6; −5).

Bài 6 trang 65 SGK Toán 12 tập 1

Gọi a là góc giữa hai vectơ $\overrightarrow u = (0; - 1;0)$ $\overrightarrow u = (0; - 1;0)$ và $\overrightarrow v = (\sqrt 3 ;1;0)$ $\overrightarrow v = (\sqrt 3 ;1;0)$. Giá trị của $\alpha$ $\alpha$ là

A. $\alpha = \frac{\pi }{6}$ $\alpha = \frac{\pi }{6}$.

B. $\alpha = \frac{\pi }{3}$ $\alpha = \frac{\pi }{3}$.

C. $\alpha = \frac{{2\pi }}{3}$ $\alpha = \frac{{2\pi }}{3}$.

D. $\alpha = \frac{\pi }{2}$ $\alpha = \frac{\pi }{2}$.

Bài 7 trang 65 SGK Toán 12 tập 1

Cho A(2; −1; 1), B(−1; 3; −1), C(5; −3; 4). Tích vô hướng $\overrightarrow {AB} . \overrightarrow {BC}$ $\overrightarrow {AB} . \overrightarrow {BC}$ có giá trị là

A. 48.

B. −48.

C. 52.

D. −52.

Bài 8 trang 65 SGK Toán 12 tập 1

Cho hai điểm A(–1; 2; 3), B = (1; 0; 2). Toạ độ điểm M thoả mãn $\overrightarrow {AB} = 2\overrightarrow {MA}$ $\overrightarrow {AB} = 2\overrightarrow {MA}$ là

A. $M( - 2;3;\frac{7}{2})$ $M( - 2;3;\frac{7}{2})$

B. $M( - 2; - 3;\frac{7}{2})$ $M( - 2; - 3;\frac{7}{2})$

C. M( - 2;3;7).

D. M( - 4;6;7).

Bài 9 trang 65 SGK Toán 12 tập 1

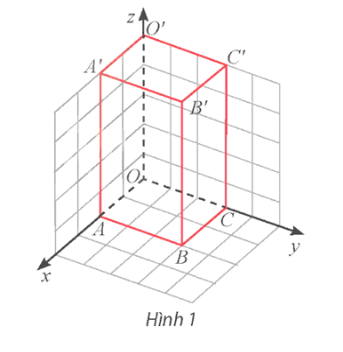
Trong không gian Oxyz, cho hình hộp chữ nhật OABC.O'A'B'C' như Hình 1, biết B'(2; 3; 5).

a) Tìm tọa độ các đỉnh còn lại của hình hộp.

b) Tính độ dài đường chéo OB' của hình hộp chữ nhật đó.

Giải Toán 12 trang 65 Chân trời

Bài 10 trang 65 SGK Toán 12 tập 1

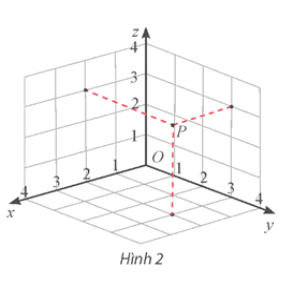
Tìm tọa độ của điểm P được biểu diễn trong Hình 2 và tính khoảng cách OP.

Giải Toán 12 trang 65 Chân trời

Xem lời giải Toán 12 trang 65

Giải Toán 12 trang 66 Chân trời

Bài 11 trang 66 SGK Toán 12 tập 1

Cho $\overrightarrow u = (2; - 5;3),\overrightarrow v = (0;2; - 1),\overrightarrow w = (1;7;2)$ $\overrightarrow u = (2; - 5;3),\overrightarrow v = (0;2; - 1),\overrightarrow w = (1;7;2)$. Tìm toạ độ của vectơ $\overrightarrow a = \overrightarrow u - 4\overrightarrow v - 2\overrightarrow w$ $\overrightarrow a = \overrightarrow u - 4\overrightarrow v - 2\overrightarrow w$.

Bài 12 trang 66 SGK Toán 12 tập 1

Cho ba điểm A(0; 1; 2), B(1; 2; 3), C(1; −2; −5). Gọi M là điểm nằm trên đoạn thẳng BC sao cho MB = 3MC. Tính độ dài đoạn thẳng AM.

Bài 13 trang 66 SGK Toán 12 tập 1

Bài 14 trang 66 SGK Toán 12 tập 1

Cho hai điểm A(1; 2; −1), B(0; −2; 3).

a) Tính độ dài đường cao AH hạ từ đỉnh A của tam giác OAB với O là gốc tọa độ.

b) Tính diện tích tam giác OAB.

Bài 15 trang 66 SGK Toán 12 tập 1

Cho biết máy bay A đang bay với vectơ vận tốc $\overrightarrow a$ $\overrightarrow a$ = (300;200;400) (đơn vị: km/h). Máy bay B bay cùng hướng và có tốc độ gấp ba lần tốc độ của máy bay A.

a) Tìm tọa độ vectơ vận tốc $\overrightarrow b$ $\overrightarrow b$ của máy bay B.

b) Tính tốc độ của máy bay B.

Bài 16 trang 66 SGK Toán 12 tập 1

Cho biết bốn đoạn thẳng nối từ một đỉnh của tứ diện đến trọng tâm mặt đối diện luôn cắt nhau tại một điểm gọi là trọng tâm của tứ diện đó.

Một phân tử metan CH4 được cấu tạo bởi bốn nguyên tử hydrogen ở các đỉnh của một tứ diện đều và một nguyên tử carbon ở trọng tâm của tứ diện.

Góc liên kết là góc tạo bởi liên kết H – C – H là góc giữa các đường nối nguyên tử carbon với hai trong số các nguyên tử hydrogen. Chứng minh rằng góc liên kết này gần bằng 109,5°.

Giải Toán 12 trang 66 Chân trời