Giải Toán 12 trang 21 tập 1 Kết nối tri thức

Giải Toán 12 trang 21 Tập 1 Kết nối tri thức hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 12 Kết nối tri thức tập 1 trang 21.

Luyện tập 1 trang 21 SGK Toán 12 tập 1 Kết nối

Tìm tiệm cận ngang của đồ thị hàm số \(y =f(x)= \frac{2x-1}{x-1}\)

Hướng dẫn giải:

Ta có:

\(\lim_{x\rightarrow +\infty} f(x)= \lim_{x\rightarrow +\infty} \frac{2x-1}{x-1} =\lim_{x\rightarrow +\infty} \frac{2 -\frac{1}{x} }{1-\frac{1}{x}} = 2\)

\(\lim_{x\rightarrow -\infty} f(x)= \lim_{x\rightarrow -\infty} \frac{2x-1}{x-1} =\lim_{x\rightarrow -\infty} \frac{ 2 -\frac{1}{x} }{ 1-\frac{1}{x}} = 2\)

Vậy đồ thị hàm số f(x) có tiệm cận ngang là đường thẳng y = 2.

Vận dụng 1 trang 21 SGK Toán 12 tập 1 Kết nối

Giải bài toán trong tình huống mở đầu.

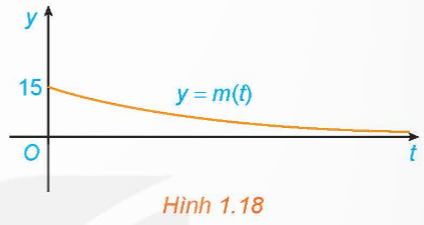
Tình huống: Giả sử khối lượng còn lại của một chất phóng xạ (gam) sau t ngày phân rã được cho bởi hàm số m(t) = 15e^{− 0,012t}. Khối lượng m(t) thay đổi ra sao khi t → +∞? Điều này thể hiện trên Hình 1.18 như thế nào?

Hướng dẫn giải:

Ta có: \(m(t)=15e^{−0,012t}=\frac{15}{e^{0,012t}}\)

Khi t → +∞ thì m(t) → 0

Trên Hình 1.18, khi t càng lớn thì m(t) càng gần trục hoành.

Hoạt động 2 trang 21 SGK Toán 12 tập 1 Kết nối

Cho hàm số \(y = f(x) = \frac{x}{x-1}\) có đồ thị (C). Với x > 1, xét điểm M (x; f(x)) thuộc (C). Gọi H là hình chiếu vuông góc của M trên đường thẳng x = 1 (H.1.22).

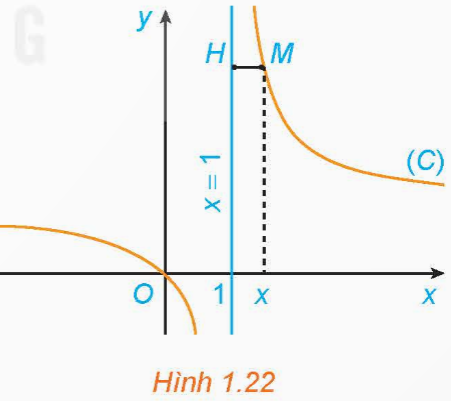
a) Tính khoảng cách MH.

b) Khi M thay đổi trên (C) sao cho khoảng cách MH dần đến 0, có nhận xét gì về tung độ của điểm M?

Hướng dẫn giải:

Đang cập nhật...

-----------------------------------------------

---> Xem thêm: Giải Toán 12 trang 22 tập 1 Kết nối tri thức

Lời giải Toán 12 trang 21 Tập 1 Kết nối tri thức với các câu hỏi nằm trong Bài 3: Đường tiệm cận của đồ thị hàm số, được VnDoc biên soạn và đăng tải!