Giải Toán 12 trang 13 tập 1 Cánh diều

Giải Toán 12 trang 13 Tập 1 hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 12 Cánh diều tập 1 trang 13.

Bài 1 trang 13 SGK Toán 12 tập 1

Cho hàm số y = f(x) có bảng biến thiên như sau:

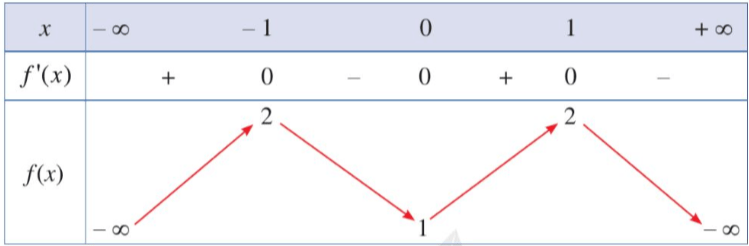
Hàm số đã cho đồng biến trên khoảng nào dưới đây?

A. (1; + ∞). B. (– 1; 0).

C. (– 1; 1). D. (0; 1).

Hướng dẫn giải:

Đáp số đúng: D

Hàm số đồng biến trên mỗi khoảng \((-\infty;-1)\) và (0; 1).

Bài 2 trang 13 SGK Toán 12 tập 1

Cho hàm số y = f(x) có bảng biến thiên như sau:

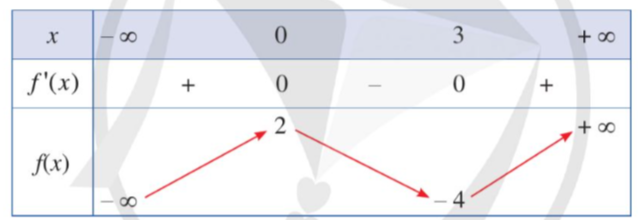
Giá trị cực tiểu của hàm số đã cho bằng

A. 2 B. 3

C. - 4 D. 0.

Hướng dẫn giải:

Đáp số đúng: C

Hàm số đạt cực tiểu tại x = 3 và giá trị cực tiểu là - 4.

Bài 3 trang 13 SGK Toán 12 tập 1

Tìm các khoảng đơn điệu của mỗi hàm số sau:

a) y = - x³ + 2x² - 3;

b) y = x⁴ + 2x² + 5;

c) \(y = \frac{3x+1}{2-x}\);

d) \(y = \frac{x^{2}-2x }{x+1}\).

Hướng dẫn giải:

a) y = - x³ + 2x² - 3

TXĐ: R

Ta có: y' = - 3x² + 4x;

y' = 0 ⇔ x = 0 hoặc \(x=\frac{4}{3}\)

Bảng biến thiên:

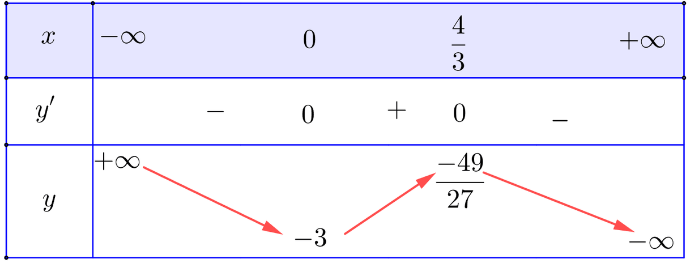
Vậy hàm số nghịch biến trên mỗi khoảng \((-\infty;0)\) và \(\left(\frac{4}{3};+ \infty \right)\); nghịch biến trên khoảng \(\left(0;\frac{4}{3}\right)\)

b) y = x⁴ + 2x² + 5

TXĐ: R

Ta có: y' = 4x³ + 4x; y' = 0 ⇔ x = 0

Bảng biến thiên:

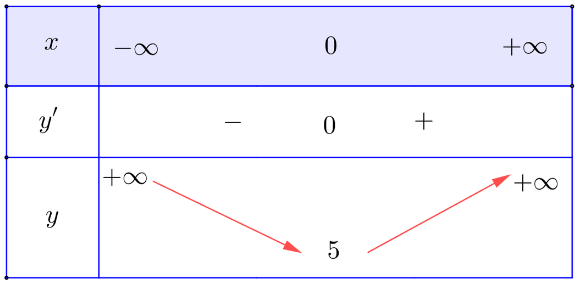
Vậy hàm số nghịch biến trên khoảng (– ∞; 0); đồng biến trên khoảng (0; + ∞).

c) \(y = \frac{3x+1}{2-x}\)

 

d) \(y = \frac{x^{2}-2x }{x+1}\)

 

Bài 4 trang 13 SGK Toán 12 tập 1

Tìm điểm cực trị của mỗi hàm số sau:

a) y = 2x³ + 3x² – 36x – 10;

b) y = – x⁴ – 2x² + 9;

c) \(y=x+\frac{1}{x}\)

Hướng dẫn giải:

a) y = 2x³ + 3x² – 36x – 10

TXĐ: R

Ta có: y' = 6x² + 6x - 36;

y' = 0 ⇔ x = - 3 hoặc x = 2.

Bảng biến thiên:

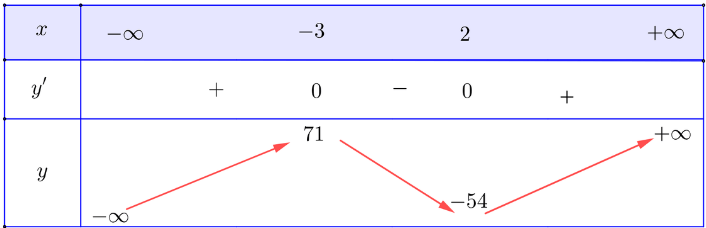
Vậy hàm số đạt cực đại tại x = - 3 và đạt cực tiểu tại x = 2.

b) y = - x⁴ - 2x² + 9

TXĐ: R

Ta có: y' = - 4x³ - 4x; y' = 0 ⇔ x = 0

Bảng biến thiên:

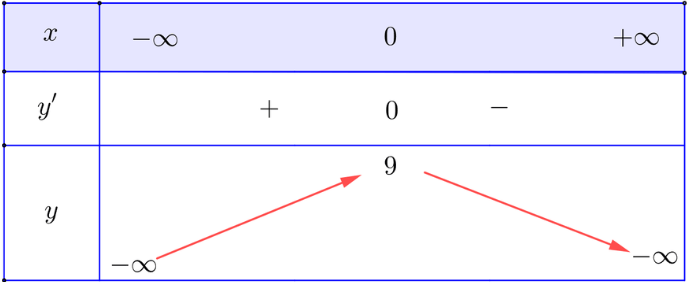
Vậy hàm số đạt cực đại tại x = 0.

c) \(y=x+\frac{1}{x}\)

-----------------------------------------------

---> Xem thêm: Giải Toán 12 trang 14 tập 1 Cánh diều

Lời giải Toán 12 trang 13 Tập 1 Cánh diều với các câu hỏi nằm trong Bài 1: Tính đơn điệu của hàm số, được VnDoc biên soạn và đăng tải!