Giải Toán 12 trang 49 tập 1 Kết nối tri thức
Giải Toán 12 trang 49 Tập 1
Giải Toán 12 trang 49 Tập 1 Kết nối tri thức hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 12 Kết nối tri thức tập 1 trang 49.
Hoạt động 3 trang 49 SGK Toán 12 tập 1 Kết nối
Trong không gian, cho hai vectơ ![]() \(\overrightarrow {a}\) và
\(\overrightarrow {a}\) và ![]() \(\overrightarrow {b}\) không cùng phương. Lấy điểm A và vẽ các vectơ
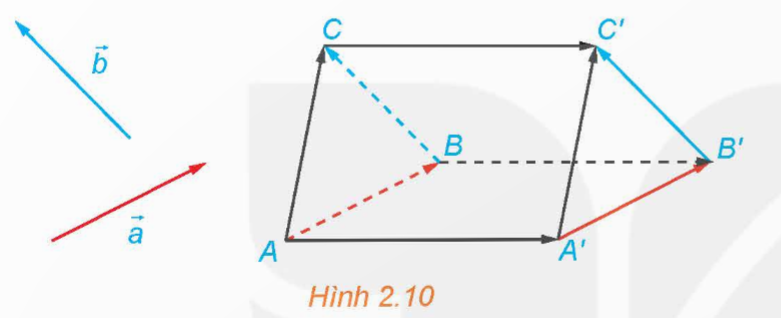
\(\overrightarrow {b}\) không cùng phương. Lấy điểm A và vẽ các vectơ ![]() \(\overrightarrow{AB} = \overrightarrow{a} ,\ \overrightarrow{BC} = \overrightarrow{b}\). Lấy điểm A' khác A và vẽ các vectơ
\(\overrightarrow{AB} = \overrightarrow{a} ,\ \overrightarrow{BC} = \overrightarrow{b}\). Lấy điểm A' khác A và vẽ các vectơ ![]() \(\overrightarrow{A'B'} = \overrightarrow{a} ,\ \overrightarrow{B'C'} = \overrightarrow{b}\) (H.2.10).
\(\overrightarrow{A'B'} = \overrightarrow{a} ,\ \overrightarrow{B'C'} = \overrightarrow{b}\) (H.2.10).
a) Giải thích vì sao ![]() \(\overrightarrow{A A'} = \overrightarrow{BB'}\) và
\(\overrightarrow{A A'} = \overrightarrow{BB'}\) và ![]() \(\overrightarrow{BB'} = \overrightarrow{CC'}\).
\(\overrightarrow{BB'} = \overrightarrow{CC'}\).
b) Giải thích vì sao AA'C'C là hình bình hành, từ đó suy ra ![]() \(\overrightarrow{AC} = \overrightarrow{A'C'}\).
\(\overrightarrow{AC} = \overrightarrow{A'C'}\).
Hướng dẫn giải:
a) Ta có: ![]() \(\overrightarrow{AB} = \overrightarrow{a}\) và
\(\overrightarrow{AB} = \overrightarrow{a}\) và ![]() \(\overrightarrow{A'B'} = \overrightarrow{a}\)
\(\overrightarrow{A'B'} = \overrightarrow{a}\)
Suy ra ![]() \(\overrightarrow{AB} = \overrightarrow{A'B'}\)
\(\overrightarrow{AB} = \overrightarrow{A'B'}\)
⇒ AB = A'B' và AB // A'B' hay ABB'A' là hình bình hành
⇒ AA' = BB' và AA' // BB'
⇒ ![]() \(\overrightarrow{AA'} = \overrightarrow{BB'}\) (hai vecto có cùng độ dài và cùng hướng)
\(\overrightarrow{AA'} = \overrightarrow{BB'}\) (hai vecto có cùng độ dài và cùng hướng)
Chứng minh tương tự, ta có ![]() \(\overrightarrow{BB'} = \overrightarrow{CC'}\)
\(\overrightarrow{BB'} = \overrightarrow{CC'}\)
b) Do ![]() \(\overrightarrow{AA'} = \overrightarrow{BB'}\) và
\(\overrightarrow{AA'} = \overrightarrow{BB'}\) và ![]() \(\overrightarrow{BB'} = \overrightarrow{CC'}\) (cma)
\(\overrightarrow{BB'} = \overrightarrow{CC'}\) (cma)
⇒ ![]() \(\overrightarrow{AA'} = \overrightarrow{CC'}\)
\(\overrightarrow{AA'} = \overrightarrow{CC'}\)
⇒ AA' = CC' và AA' // CC' hay ACC'A' là hình bình hành
⇒ AC = A'C' và AC // A'C'
⇒ ![]() \(\overrightarrow{AC} = \overrightarrow{A'C'}\) (hai vecto có cùng độ dài và cùng hướng)
\(\overrightarrow{AC} = \overrightarrow{A'C'}\) (hai vecto có cùng độ dài và cùng hướng)
-----------------------------------------------
---> Bài tiếp theo: Giải Toán 12 trang 50 tập 1 Kết nối tri thức
Lời giải Toán 12 trang 49 Tập 1 Kết nối tri thức với các câu hỏi nằm trong Bài 6: Vectơ trong không gian, được VnDoc biên soạn và đăng tải!









