Toán 12 Cánh diều bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
Giải bài tập Toán 12 CD bài 2
VnDoc.com xin gửi tới bạn đọc bài viết Toán 12 Cánh diều bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số để bạn đọc cùng tham khảo. Bài viết với hướng dẫn giải bài tập SGK Toán 12 Cánh diều tập 1 các trang 15, 16, 17, 18, 19, 20.
Giải Toán 12 trang 15 Cánh diều
Câu hỏi khởi động trang 15 SGK Toán 12 tập 1
Cho một tấm nhôm có dạng hình vuông cạnh 6 dm. Bác Ánh cắt ở bốn góc bốn hình vuông có cùng độ dài cạnh bằng x (dm), rồi gập tấm nhôm lại như Hình 7 để được một cái hộp có dạng hình hộp chữ nhật không có nắp. Gọi V là thể tích của khối hộp đó.
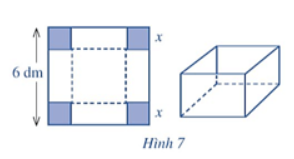
V được tính theo x bởi công thức nào? Có thể tìm giá trị lớn nhất của V bằng cách nào?
Hoạt động 1 trang 15 SGK Toán 12 tập 1
Cho hàm số y = f(x) liên tục trên đoạn [– 1; 1] và có đồ thị là đường cong ở Hình 8.
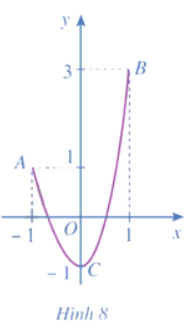
Quan sát đồ thị và cho biết:
a) Điểm nào thuộc đồ thị hàm số có tung độ lớn nhất;
b) Điểm nào thuộc đồ thị hàm số có tung độ nhỏ nhất.
Xem lời giải Toán 12 trang 15
Giải Toán 12 trang 16 Cánh diều
Luyện tập 1 trang 16 SGK Toán 12 tập 1
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số 
\(f(x) = \sqrt{9-x^{2} }\) trên đoạn [– 3; 3]
Luyện tập 2 trang 16 SGK Toán 12 tập 1
Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của hàm số \(y = \frac{2x-5}{x-1}\) trên nửa khoảng (1; 3]
Xem lời giải Toán 12 trang 16
Giải Toán 12 trang 17 Cánh diều
Hoạt động 3 trang 17 SGK Toán 12 tập 1
Cho hàm số y = f(x) = 2x3 – 6x, x ∈ [– 2; 2] có đồ thị là đường cong ở Hình 9
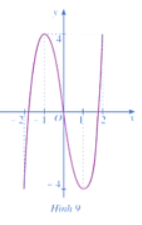
a) Dựa vào đồ thị ở Hình 9, hãy cho biết các giá trị \(M = \mathop {\max }\limits_{\left[ { - 2;2} \right]} f\left( x \right);m = \mathop {\min }\limits_{\left[ { - 2;2} \right]} f\left( x \right)\) bằng bao nhiêu.
b) Giải phương trình \(f'\left( x \right) = 0\) với \(x \in \left( { - 2;2} \right)\)
c) Tính các giá trị của hàm số f(x) tại hai đầu mút x = – 2; x = 2 và tại các điểm x ∈ (–2; 2) mà ở đó f'(x) = 0.
d) So sánh M (hoặc m) với số lớn nhất (hoặc số bé nhất) trong các giá trị tính được ở câu c.
Xem lời giải Toán 12 trang 17
Giải Toán 12 trang 18 Cánh diều
Luyện tập 3 trang 18 SGK Toán 12 tập 1
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x) = sin 2x – 2x trên đoạn \(\begin{bmatrix} \frac{\pi }{2} ;\frac{3\pi }{2} \end{bmatrix}\)
Xem lời giải Toán 12 trang 18
Giải Toán 12 trang 19 Cánh diều
Bài 1 trang 19 SGK Toán 12 tập 1
Nếu hàm số y = f(x) có đạo hàm trên ℝ thỏa mãn f'(x) = sin x – 2 023, ∀ x ∈ ℝ thì giá trị lớn nhất của hàm số y = f(x) trên đoạn [1; 2] bằng
A. f(0).
B. f(1).
C. f(1,5).
D. f(2).
Xem lời giải Toán 12 trang 19
Giải Toán 12 trang 20 Cánh diều
Bài 2 trang 20 SGK Toán 12 tập 1
Tìm giá trị lớn nhất của mỗi hàm số sau:
a) \(f(x) = \frac{4}{1+x^{2} }\)
b) \(f(x) = x - \frac{3}{x}\) trên nửa khoảng (0; 3].
Bài 3 trang 20 SGK Toán 12 tập 1
Tìm giá trị nhỏ nhất của mỗi hàm số sau:
a) f(x) = x + \(\frac{4}{x}\) trên khoảng (0; + ∞);
b) f(x) = x3 – 12x + 1 trên khoảng (1; + ∞).
Bài 4 trang 20 SGK Toán 12 tập 1
Tìm giá trị lớn nhất và giá trị nhỏ nhất của mỗi hàm số sau:
a) f(x) = x3 − \(\frac{3}{2}\)x2 trên đoạn [– 1; 2];
b) f(x) = x4 – 2x3 + x2 + 1 trên đoạn [– 1; 1];
c) f(x) = ex(x2 – 5x + 7) trên đoạn [0; 3];
d) f(x) = cos2x + 2x + 1 trên đoạn [\(\frac{-\pi }{2}\);π].
Bài 5 trang 20 SGK Toán 12 tập 1
Trong 5 giây đầu tiên, một chất điểm chuyển động theo phương trình
s(t) = – t3 + 6t2 + t + 5,
trong đó t tính bằng giây và s tính bằng mét. Chất điểm có vận tốc tức thời lớn nhất bằng bao nhiêu trong 5 giây đầu tiên đó?
Bài 6 trang 20 SGK Toán 12 tập 1
Người ta bơm xăng vào bình của một xe ô tô. Biết rằng thể tích V (lít) của lượng xăng trong bình xăng tính theo thời gian bơm xăng t (phút) được cho bởi công thức
V(t) = 300(t2 – t3) + 4 với 0 ≤ t ≤ 0,5.
(Nguồn: R.I Charles et al., Algebra 2, Pearson)
a) Ban đầu trong bình xăng có bao nhiêu lít xăng?
b) Sau khi bơm 30 giây thì bình xăng đầy. Hỏi dung tích của bình xăng trong xe là bao nhiêu lít?
c) Khi xăng chảy vào bình xăng, gọi V'(t) là tốc độ tăng thể tích tại thời điểm t với 0 ≤ t ≤ 0,5. Xăng chảy vào bình xăng ở thời điểm nào có tốc độ tăng thể tích là lớn nhất.
Bài 7 trang 20 SGK Toán 12 tập 1
Ho ép khí quản co lại, ảnh hưởng đến tốc độ của không khí đi vào khí quản. Tốc độ của không khí đi vào khí quản khi ho được cho bởi công thức
V = k(R – r)r2 với 0 ≤ r < R,
trong đó k là hằng số, R là bán kính bình thường của khí quản, r là bán kính khí quản khi ho (Nguồn: R. Larson and B. Edwards, Calculus 10e, Cengage 2014). Hỏi bán kính của khí quản khi ho bằng bao nhiêu thì tốc độ của không khí đi vào khí quản là lớn nhất?
Xem lời giải Toán 12 trang 20
Bài tiếp theo: Toán 12 Cánh diều bài 3: Đường tiệm cận của đồ thị hàm số
