Giải Toán 12 trang 88 tập 1 Cánh diều
Giải Toán 12 trang 88 Cánh diều Tập 1
Giải Toán 12 trang 88 Tập 1 hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 12 Cánh diều tập 1 trang 88.
Bài 1 trang 88 SGK Toán 12 tập 1
Bảng 8 biểu diễn mẫu số liệu ghép nhóm về số tiền (đơn vị: nghìn đồng) mà 60 khách hàng mua sách ở một cửa hàng trong một ngày.
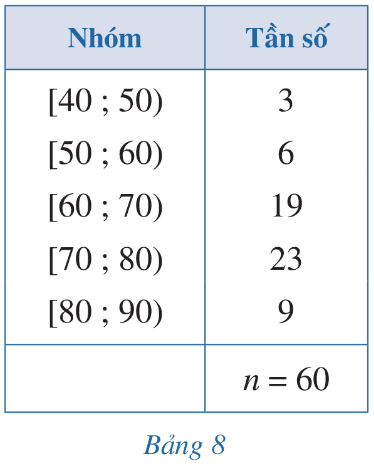
a) Khoảng biến thiên của mẫu số liệu ghép nhóm trên là:
A. 50.
B. 30.
C. 6.
D. 69,8.
b) Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên là:
A. 50.
B. 40.
C. 14,23.
D. 70,87.
Hướng dẫn giải:
a) Đáp án đúng: A
Khoảng biến thiên của mẫu số liệu ghép nhóm là: 90 – 40 = 50
b) Đáp án đúng: C
| Nhóm | Tần số | Tần số tích lũy |
[40; 50) [50; 60) [60; 70) [70; 80) [80; 90) | 3 6 19 23 9 | 3 9 28 51 60 |
n = 60 |
Số phần tử của mẫu là n = 60.
Ta có: 
\(\frac{n}{4}=\frac{60}{4}=15\) mà 9 < 15 < 28. Suy ra nhóm 3 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 15. Xét nhóm 3 là nhóm [60; 70) có s = 60; h = 10; n3 = 19 và cf2 = 9.
Áp dụng công thức, ta có tứ phân vị thứ nhất là:
\({Q_1}=60+\left({\frac{{15-9}}{19}}\right).10=\frac{1200}{19}\)
Ta có: \(\frac{3n}{4}=\frac{3.60}{4}=45\) mà 28 < 45 < 51. Suy ra nhóm 4 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 45. Xét nhóm 4 là nhóm [70; 80) có t = 70; l = 10; n4 = 23 và cf3 = 28.
Áp dụng công thức, ta có tứ phân vị thứ ba là:
\({Q_3}=70+\left({\frac{{45-28}}{23}}\right).10=\frac{1780}{23}\)
Vậy khoảng tứ phân vị của mẫu số liệu ghép nhóm đã cho là:
ΔQ = Q3 – Q1 = \(\frac{1780}{23}-\frac{1200}{19}\)≈ 14,23
Bài 2 trang 88 SGK Toán 12 tập 1
Bảng 9 biểu diễn mẫu số liệu ghép nhóm thống kê mức lương của một công ty (đơn vị: triệu đồng).
a) Tính khoảng biến thiên của mẫu số liệu ghép nhóm đó.
b) Tính khoảng tứ phân vị của mẫu số liệu ghép nhóm đó.
Hướng dẫn giải:
a) Khoảng biến thiên của mẫu số liệu ghép nhóm là: 40 – 10 = 30
b)
| Nhóm | Tần số | Tần số tích lũy |
[10; 15) [15; 20) [20; 25) [25; 30) [30; 35) [35; 40) | 15 18 10 10 5 2 | 15 33 43 53 58 60 |
n = 60 |
Số phần tử của mẫu là n = 60.
Ta có: \(\frac{n}{4}=\frac{60}{4}=15\) mà 15 ≤ 15 < 33. Suy ra nhóm 1 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 15. Xét nhóm 1 là nhóm [10; 15) có s = 10; h = 5; n1 = 15 và cf0 = 0.
Áp dụng công thức, ta có tứ phân vị thứ nhất là:
\({Q_1}=10+\left({\frac{{15-0}}{15}}\right).5=15\)
Ta có: \(\frac{3n}{4}=\frac{3.60}{4}=45\) mà 43 < 45 < 53. Suy ra nhóm 4 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 45. Xét nhóm 4 là nhóm [25; 30) có t = 25; l = 5; n4 = 10 và cf3 = 43.
Áp dụng công thức, ta có tứ phân vị thứ ba là:
\({Q_3}=25+\left({\frac{{45-43}}{10}}\right).5=26\)
Vậy khoảng tứ phân vị của mẫu số liệu ghép nhóm đã cho là:
ΔQ = Q3 – Q1 = 26 – 15 = 11
Bài 3 trang 88 SGK Toán 12 tập 1
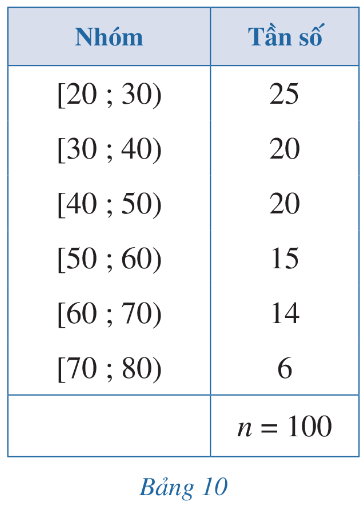
Bảng 10 biểu diễn mẫu số liệu ghép nhóm về độ tuổi của cư dân trong một khu phố.
a) Tính khoảng biến thiên của mẫu số liệu ghép nhóm đó.
b) Tính khoảng tứ phân vị của mẫu số liệu ghép nhóm đó.
Hướng dẫn giải:
a) Khoảng biến thiên của mẫu số liệu ghép nhóm là: 80 – 20 = 60
b)
| Nhóm | Tần số | Tần số tích lũy |
[20; 30) [30; 40) [40; 50) [50; 60) [60; 70) [70; 80) | 25 20 20 15 14 6 | 25 45 65 80 94 100 |
n = 100 |
Số phần tử của mẫu là n = 100.
Ta có: \(\frac{n}{4}=\frac{100}{4}=25\) mà 25 ≤ 25. Suy ra nhóm 1 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 25. Xét nhóm 1 là nhóm [20; 30) có s = 20; h = 10; n1 = 25 và cf0 = 0.
Áp dụng công thức, ta có tứ phân vị thứ nhất là:
\({Q_1}=20+\left({\frac{{25-0}}{25}}\right).10=30\)
Ta có: \(\frac{3n}{4}=\frac{3.100}{4}=75\) mà 65 < 75 < 80. Suy ra nhóm 4 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 75. Xét nhóm 4 là nhóm [50; 60) có t = 50; l = 10; n4 = 15 và cf3 = 65.
Áp dụng công thức, ta có tứ phân vị thứ ba là:
\({Q_3}=50+\left({\frac{{75-65}}{15}}\right).10=\frac{170}{3}\)
Vậy khoảng tứ phân vị của mẫu số liệu ghép nhóm đã cho là:
ΔQ = Q3 – Q1 = \(\frac{170}{3}-30=\frac{80}{3}\)
-----------------------------------------------
---> Xem thêm: Giải Toán 12 trang 89 tập 1 Cánh diều
Lời giải Toán 12 trang 88 Tập 1 Cánh diều với các câu hỏi nằm trong Toán 12 Cánh diều Bài 1: Khoảng biến thiên, khoảng tứ phân vị của mẫu số liệu ghép nhóm, được VnDoc biên soạn và đăng tải!
