VnDoc.com

Giải Toán 12 trang 18 tập 1 Chân trời sáng tạo

Bài trước

Bài sau

Giải Toán 12 trang 18 Tập 1

Thực hành 2 trang 18 SGK Toán 12 tập 1 Chân trời
Thực hành 3 trang 18 SGK Toán 12 tập 1 Chân trời
Bài 1 trang 18 SGK Toán 12 tập 1 Chân trời
Bài 2 trang 18 SGK Toán 12 tập 1 Chân trời
Bài 3 trang 18 SGK Toán 12 tập 1 Chân trời
Bài 4 trang 18 SGK Toán 12 tập 1 Chân trời
Bài 5 trang 18 SGK Toán 12 tập 1 Chân trời
Bài 6 trang 18 SGK Toán 12 tập 1 Chân trời
Bài 7 trang 18 SGK Toán 12 tập 1 Chân trời

Giải Toán 12 trang 18 Tập 1 hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 12 Chân trời sáng tạo tập 1 trang 18.

Thực hành 2 trang 18 SGK Toán 12 tập 1 Chân trời

Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số $g(x) = x + \frac{4}{x^{2} }$ $g(x) = x + \frac{4}{x^{2} }$ trên đoạn [1; 4].

Hướng dẫn giải:

Ta có: $g'\left(x\right)=1-\frac{8}{x^3}$

g'(x) = 0 ⇔ x = 2

g(1) = 5; g(2) = 3; $g(4)=\frac{17}{4}$ $g(4)=\frac{17}{4}$

Vậy $\underset{[1;4]}{\max} g(x) = g(1)=5$ $\underset{[1;4]}{\max} g(x) = g(1)=5$ và $\underset{[1;4]}{\min} g(x) = g(2) = 3$ $\underset{[1;4]}{\min} g(x) = g(2) = 3$

Thực hành 3 trang 18 SGK Toán 12 tập 1 Chân trời

Tam giác vuông có cạnh huyền bằng 5 cm có thể có diện tích lớn nhất bằng bao nhiêu?

Hướng dẫn giải:

Giả sử độ dài một cạnh góc vuông là x (cm) (0 < x < 5)

=> Độ dài cạnh góc vuông còn lại là $\sqrt{25-x^2}$ $\sqrt{25-x^2}$ (cm)

Hàm số biểu thị diện tích tam giác là: $S\left(x\right)=\frac{ 1}{ 2} x\sqrt{25-x^2}$ $S\left(x\right)=\frac{ 1}{ 2} x\sqrt{25-x^2}$

Ta có: $S'\left(x\right)=\frac{1}{2}\left(\sqrt{25-x^2}-\frac{x^2}{\sqrt{25-x^2}}\right)$

S'(x) = 0 ⇔ $x=\frac{5}{\sqrt{2}}$ $x=\frac{5}{\sqrt{2}}$ (vì 0 < x < 5)

Lập bảng biến thiên của hàm số S(x):

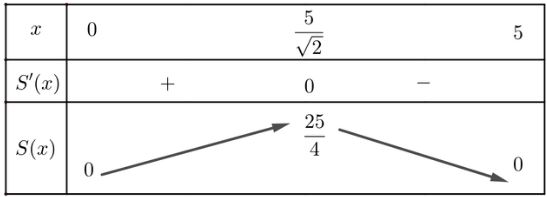
Vậy S(x) lớn nhất khi $x=\frac{5}{\sqrt{2}}$ $x=\frac{5}{\sqrt{2}}$.

Bài 1 trang 18 SGK Toán 12 tập 1 Chân trời

Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số có đồ thị được cho ở Hình 5.

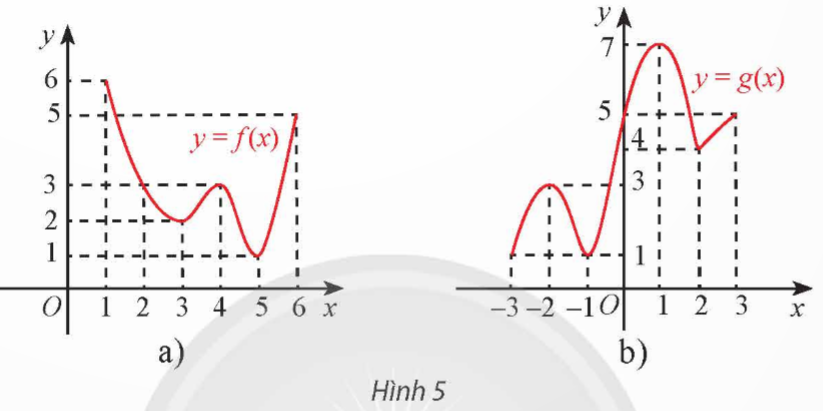
Hướng dẫn giải:

a) $\underset{[1;6]}{\max} f(x)=f(1)=6; \ \underset{[1;6]}{\min} f(x)=f(5)=1;$ $\underset{[1;6]}{\max} f(x)=f(1)=6; \ \underset{[1;6]}{\min} f(x)=f(5)=1;$

b) $\underset{[-3;3]}{\max} g(x)=g(1)=7$ $\underset{[-3;3]}{\max} g(x)=g(1)=7$

$\underset{[-3;3]}{\min} g(x)=g(-3) =g(-1)=1;$ $\underset{[-3;3]}{\min} g(x)=g(-3) =g(-1)=1;$

Bài 2 trang 18 SGK Toán 12 tập 1 Chân trời

Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:

a) y = x³ – 12x + 1 trên đoạn [−1; 3];

b) y = − x³ + 24x² – 180x + 400 trên đoạn [3; 11];

c) $y = \frac{2x+1}{x-2}$ $y = \frac{2x+1}{x-2}$ trên đoạn [3; 7];

d) y = sin2x trên đoạn $[0;\frac{7\pi }{12} ]$ $[0;\frac{7\pi }{12} ]$

Hướng dẫn giải:

a) y = x³ – 12x + 1 trên đoạn [−1; 3]

Ta có: y' = 3x² - 12

y' = 0 ⇔ x = 2 (vì x ∈ [−1; 3])

y(- 1) = 12; y(2) = - 15; y(3) = - 8

Do đó $\underset{[-1;3]}{\max} y=y(-1)=12; \ \underset{[-1;3]}{\min} y=y(2)=-15;$ $\underset{[-1;3]}{\max} y=y(-1)=12; \ \underset{[-1;3]}{\min} y=y(2)=-15;$

b) y = − x³ + 24x² – 180x + 400 trên đoạn [3; 11]

Ta có: y' = - 3x² + 48x - 180

y' = 0 ⇔ x = 6 hoặc x = 10

y(3) = 49; y(6) = - 32; y(10) = 0; y(11) = - 7

Do đó $\underset{[3;11]}{\max} y=y(3)=49; \ \underset{[3;11]}{\min} y=y(6)=-32$ $\underset{[3;11]}{\max} y=y(3)=49; \ \underset{[3;11]}{\min} y=y(6)=-32$

c) $y = \frac{2x+1}{x-2}$ $y = \frac{2x+1}{x-2}$ trên đoạn [3; 7]

Ta có: $y=-\frac{5}{\left(x-1\right)^2}<0$ $y=-\frac{5}{\left(x-1\right)^2}<0$ với mọi x ∈ [3; 7].

Do đó $\underset{[3;7]}{\max} y=y(3)=7; \ \underset{[3;]}{\min} y=y(7)=3$ $\underset{[3;7]}{\max} y=y(3)=7; \ \underset{[3;]}{\min} y=y(7)=3$

d) y = sin2x trên đoạn $[0;\frac{7\pi }{12} ]$ $[0;\frac{7\pi }{12} ]$

Bài 3 trang 18 SGK Toán 12 tập 1 Chân trời

Tìm giá trị nhỏ nhất của các hàm số sau:

a) y = x³ – 3x – 4 trên nửa khoảng [− 3; 2);

b) $y = \frac{3x^{2} -4x}{x^{2} -1}$ $y = \frac{3x^{2} -4x}{x^{2} -1}$ trên khoảng (−1; +∞).

Hướng dẫn giải:

a) y = x³ – 3x – 4 trên nửa khoảng [−3; 2);

Ta có: y' = 3x² - 3x

y' = 0 ⇔ x = - 1 hoặc x = 1

Bảng biến thiên:

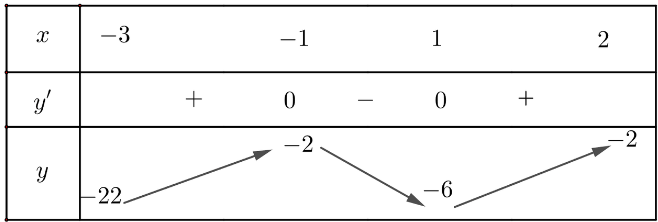
Từ bảng biến thiên, ta có: $\underset{[-3;2]}{\max} y=y(-1)=-2; \ \underset{[-3;2]}{\min} y=y(-3)=-22;$ $\underset{[-3;2]}{\max} y=y(-1)=-2; \ \underset{[-3;2]}{\min} y=y(-3)=-22;$

b) $y = \frac{3x^{2} -4x}{x^{2} -1}$ $y = \frac{3x^{2} -4x}{x^{2} -1}$ trên khoảng (−1; +∞).

TXĐ: D = (−1; +∞) \ {1}

Ta có: $y'=\frac{4x^2-6x+4}{\left(x^2-1\right)^2}>0$ với mọi x thuộc D

Bảng biến thiên:

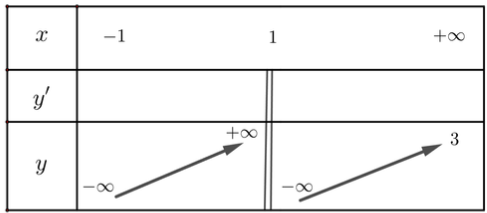
Từ bảng biến thiên, hàm số không có giá trị nhỏ nhất.

Bài 4 trang 18 SGK Toán 12 tập 1 Chân trời

Khi làm nhà kho, bác An muốn cửa số có dạng hình chữ nhật với chu vi bằng 4 m (Hình 6). Tìm kích thước khung cửa sổ sao cho diện tích cửa sổ lớn nhất (để hứng được nhiều ánh sáng nhất)?

Hướng dẫn giải:

Nửa chu vi của cửa sổ là: 2 m

Gọi x (m) là chiều dài của cửa sổ. (0 < x < 2)

=> Chiều rộng của cửa sổ là: 2 - x (m)

Diện tích cửa sổ là: x(2 - x) = 2x - x² (m²)

Xét hàm số y = S(x) = 2x - x² (0 < x < 2)

Ta có: y' = 2 - 2x; y' = 0 ⇔ x = 1

Bảng biến thiên:

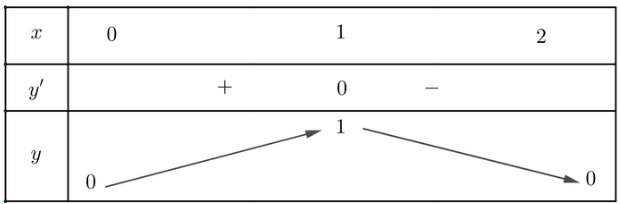
Vậy diện tích khung cửa sổ lớn nhất là 1m² khi x = 1, tức là khung cửa sổ có dạng hình vuông cạnh 1m.

Bài 5 trang 18 SGK Toán 12 tập 1 Chân trời

Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số

$y = 2\sqrt{1-x^{2} } +x^{2}$ $y = 2\sqrt{1-x^{2} } +x^{2}$

Hướng dẫn giải:

$y = 2\sqrt{1-x^{2} } +x^{2}$ $y = 2\sqrt{1-x^{2} } +x^{2}$

Tập xác định: [- 1; 1]

Ta có: $y'=2x-\frac{2x}{\sqrt{1-x^2}}$; y' = 0 ⇔ x = 0

y(- 1) = 1; y(0) = 2; y(1) = 1

Do đó $\underset{[-1;1]}{\max} y=y(0)=2; \ \underset{[-1;1]}{\min} y=y(-1)=y(1)=1$ $\underset{[-1;1]}{\max} y=y(0)=2; \ \underset{[-1;1]}{\min} y=y(-1)=y(1)=1$.

Bài 6 trang 18 SGK Toán 12 tập 1 Chân trời

Khối lượng q (kg) của một mặt hàng mà cửa tiệm bán được trong một ngày phụ thuộc vào giá bán p (nghìn đồng/kg) theo công thức $p=15-\frac{1}{2}q$ $p=15-\frac{1}{2}q$. Doanh thu từ việc bán mặt hàng trên của cửa tiệm được tính theo công thức R = pq.

a) Viết công thức biểu diễn R theo p.

b) Tìm giá bán mỗi kilôgam sản phẩm để đạt được doanh thu cao nhất và xác định doanh thu cao nhất đó.

Hướng dẫn giải:

a) Ta có: $p=15-\frac{1}{2}q$ $p=15-\frac{1}{2}q$ ⇒ q = 30 – 2p

Doanh thu từ việc bán mặt hàng trên của cửa tiệm là:

$R = pq = p(30 - 2p) = 30p - 2p^2$

b) Xét hàm số $y = R(p) = 30p - 2p^2$

Tập xác định của hàm số: $(0; +\infty)$ $(0; +\infty)$

Ta có: y' = 30 – 4p; y' = 0 ⇔ $p=\frac{15}{2}$ $p=\frac{15}{2}$

Lập bảng biến thiên của hàm số:

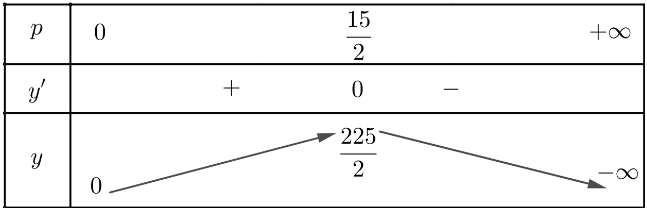
Vậy cửa tiệm đạt doanh thu cao nhất là $\frac{225}{2}$ $\frac{225}{2}$ nghìn đồng nếu giá bán là $\frac{15}{2}$ $\frac{15}{2}$ nghìn đồng/kg.

Bài 7 trang 18 SGK Toán 12 tập 1 Chân trời

Hộp sữa 1 l được thiết kế dạng hình hộp chữ nhật với đáy là hình vuông cạnh x cm. Tìm x để diện tích toàn phần của hộp nhỏ nhất.

Hướng dẫn giải:

Đổi 1 lít = 1 000 cm³.

Diện tích đáy là: S_đáy = x² (cm²)

Thể tích hộp sữa: V = S_đáy . h = 1 000 (cm³) ⇒ $h=\frac{1\ 000}{x^2}$ $h=\frac{1\ 000}{x^2}$ (cm)

Diện tích toàn phần của hộp sữa là:

$2x^2+4xh=2x^2+\frac{4\ 000}{x}$ $2x^2+4xh=2x^2+\frac{4\ 000}{x}$ (cm²)

Xét hàm số $y = S(x) = 2x^2+\frac{4\ 000}{x}$ $y = S(x) = 2x^2+\frac{4\ 000}{x}$ với x > 0.

Ta có: $y'=4x-\frac{4\ 000}{x^2}$

y' = 0 ⇔ x = 10 (vì x > 0)

Lập bảng biến thiên của hàm số y = S(x):

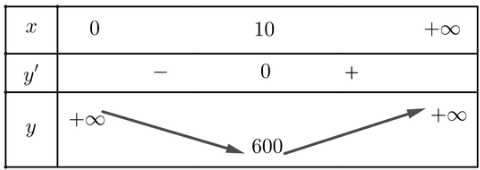
Vậy để diện tích toàn phần của hộp nhỏ nhất thì đáy là hình vuông cạnh 10 cm.

-----------------------------------------------

---> Xem thêm: Giải Toán 12 trang 19 tập 1 Chân trời sáng tạo

Lời giải Toán 12 trang 18 Tập 1 Chân trời sáng tạo với các câu hỏi nằm trong Bài 2: Giá trị lớn nhất, giá trị nhỏ nhất của hàm số, được VnDoc biên soạn và đăng tải!

Chia sẻ, đánh giá bài viết

1

1.147

Bài trước

Bài sau