Giải Toán 12 trang 21 tập 1 Cánh diều

Giải Toán 12 trang 21 Tập 1 hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 12 Cánh diều tập 1 trang 21.

Câu hỏi khởi động trang 21 SGK Toán 12 tập 1

Số dân của một thị trấn sau x năm kể từ năm 1970 được ước tính bởi công thức

\(y = f(x) = \frac{26x+10}{x+5}\)

(f(x) được tính bằng nghìn người) (Nguồn: Giải tích 12 Nâng cao, NXBGD Việt Nam, 2020). Xem y = f(x) là một hàm số xác định trên nửa khoảng [0; + ∞), đồ thị của hàm số đó là đường cong màu xanh ở Hình 10.

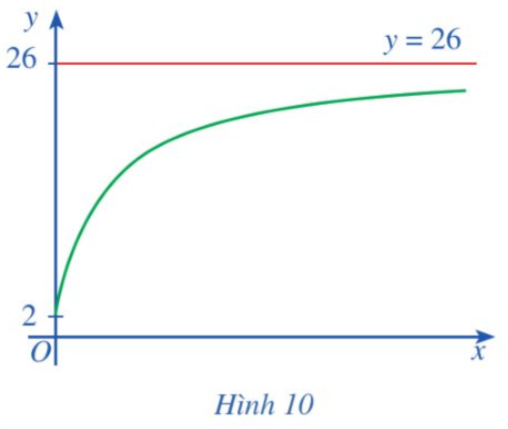
Khi x → + ∞, đồ thị hàm số y = f(x) ngày càng “tiến gần” tới đường thẳng nào?

Hướng dẫn giải:

Khi x → + ∞, đồ thị hàm số y = f(x) ngày càng “tiến gần” tới đường thẳng y = 26.

Hoạt động 1 trang 21 SGK Toán 12 tập 1

Xét hàm số \(y = f(x) = \frac{26x+10}{x+5}\), với x ∈ [0; + ∞) có đồ thị là đường cong ở Hình 10 trong bài toán mở đầu. Tìm \(\lim_{x\rightarrow+\infty } f(x)\).

Hướng dẫn giải:

Ta có: \(\lim_{x\rightarrow +\infty} f(x) = \lim_{x\rightarrow +\infty} \frac{26x+10}{x+5} =26\)

-----------------------------------------------

---> Xem thêm: Giải Toán 12 trang 22 tập 1 Cánh diều

Lời giải Toán 12 trang 21 Tập 1 Cánh diều với các câu hỏi nằm trong Bài 3: Đường tiệm cận của đồ thị hàm số, được VnDoc biên soạn và đăng tải!