Giải Toán 12 trang 59 tập 1 Chân trời sáng tạo

Giải Toán 12 trang 59 Tập 1

Thực hành 1 trang 59 SGK Toán 12 tập 1 Chân trời
Vận dụng 1 trang 59 SGK Toán 12 tập 1 Chân trời
Hoạt động 2 trang 59 SGK Toán 12 tập 1 Chân trời

Giải Toán 12 trang 59 Tập 1 hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 12 Chân trời sáng tạo tập 1 trang 59.

Thực hành 1 trang 59 SGK Toán 12 tập 1 Chân trời

Cho ba vectơ $\overrightarrow{a}=(2;-5;3),\overrightarrow{b}=(0;2;-1),\overrightarrow{c}=(1;7;2)$ $\overrightarrow{a}=(2;-5;3),\overrightarrow{b}=(0;2;-1),\overrightarrow{c}=(1;7;2)$

a) Tìm toạ độ của vectơ $\overrightarrow{d}=4\overrightarrow{a}-\frac{1}{3}\overrightarrow{b}+3\overrightarrow{c\ }$ $\overrightarrow{d}=4\overrightarrow{a}-\frac{1}{3}\overrightarrow{b}+3\overrightarrow{c\ }$

b) Tìm toạ độ của vectơ $\overrightarrow{e}=\overrightarrow{a}-4\overrightarrow{b}-2\overrightarrow{c\ }$ $\overrightarrow{e}=\overrightarrow{a}-4\overrightarrow{b}-2\overrightarrow{c\ }$

c) Chứng minh $\overrightarrow{a\ }$ $\overrightarrow{a\ }$ cùng phương với vectơ $\overrightarrow m = ( - 6;15; - 9)$ $\overrightarrow m = ( - 6;15; - 9)$

Hướng dẫn giải:

a) Ta có: $4\overrightarrow{a}=(8;-20;12),\frac{1}{3}\overrightarrow{b}=(0;\frac{2}{3};-\frac{1}{3}),3\overrightarrow{c}=(3;21;6)$ $4\overrightarrow{a}=(8;-20;12),\frac{1}{3}\overrightarrow{b}=(0;\frac{2}{3};-\frac{1}{3}),3\overrightarrow{c}=(3;21;6)$

Vậy $\overrightarrow{d}=4\overrightarrow{a}-\frac{1}{3}\overrightarrow{b}+3\overrightarrow{c\ }=\left(11;\frac{1}{3};\frac{55}{3}\right)$ $\overrightarrow{d}=4\overrightarrow{a}-\frac{1}{3}\overrightarrow{b}+3\overrightarrow{c\ }=\left(11;\frac{1}{3};\frac{55}{3}\right)$

b) $\overrightarrow{e}=\overrightarrow{a}-4\overrightarrow{b}-2\overrightarrow{c\ }=\left(0;-27;3\right)$ $\overrightarrow{e}=\overrightarrow{a}-4\overrightarrow{b}-2\overrightarrow{c\ }=\left(0;-27;3\right)$

c) Ta có: $\overrightarrow{m}=(-6;15;-9)=-3\left(2;-5;3\right)=-3\overrightarrow{a\ }$ $\overrightarrow{m}=(-6;15;-9)=-3\left(2;-5;3\right)=-3\overrightarrow{a\ }$

Vậy $\overrightarrow{a\ }$ $\overrightarrow{a\ }$ cùng phương với $\overrightarrow{m\ }$ $\overrightarrow{m\ }$.

Vận dụng 1 trang 59 SGK Toán 12 tập 1 Chân trời

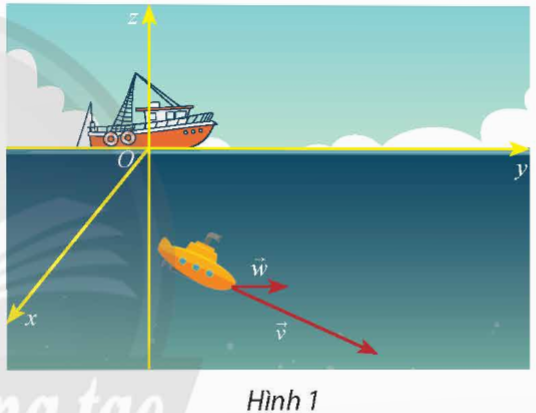
Một thiết bị thăm dò đáy biển đang lặn với vận tốc $\overrightarrow{v}=(10;8;-3)$ $\overrightarrow{v}=(10;8;-3)$ (Hình 1). Cho biết vận tốc của dòng hải lưu của vùng biển là $\overrightarrow w = (3,5;1;0)$ $\overrightarrow w = (3,5;1;0)$

a) Tìm toạ độ của vectơ tổng hai vận tốc $\overrightarrow{v\ }$ $\overrightarrow{v\ }$ và $\overrightarrow{v\ }$ $\overrightarrow{v\ }$

b) Giả sử thiết bị thăm dò lặn với vận tốc $\overrightarrow u = (7;2;0)$ $\overrightarrow u = (7;2;0)$, hãy nêu nhận xét về vectơ vận tốc của nó so với vectơ vận tốc của dòng hải lưu.

Hướng dẫn giải:

a) Ta có: $\overrightarrow{v} +\overrightarrow w=(13,5;9;-3)$ $\overrightarrow{v} +\overrightarrow w=(13,5;9;-3)$

b) $\overrightarrow{u}=(7;2;0)=2\left(3,5;1;0\right)=2\overrightarrow{w\ }$ $\overrightarrow{u}=(7;2;0)=2\left(3,5;1;0\right)=2\overrightarrow{w\ }$

Vậy vectơ vận tốc của nó cùng hướng với vectơ vận tốc của dòng hải lưu.

Hoạt động 2 trang 59 SGK Toán 12 tập 1 Chân trời

Cho hai vectơ $\overrightarrow{a}=(a_1;a_2;a_3),\overrightarrow{b}=(b_1;b_2;b_3)$ $\overrightarrow{a}=(a_1;a_2;a_3),\overrightarrow{b}=(b_1;b_2;b_3)$.

a) Biểu diễn từng vectơ $\overrightarrow{a\ }$ $\overrightarrow{a\ }$ và $\overrightarrow{b\ }$ $\overrightarrow{b\ }$ theo ba vectơ $\overrightarrow{i},\overrightarrow{j},\overrightarrow{k\ }$ $\overrightarrow{i},\overrightarrow{j},\overrightarrow{k\ }$

b) Tính các tích vô hướng $\overrightarrow{i}^2,\ \overrightarrow{j}^2,\ \overrightarrow{k}^2,\ \overrightarrow{i}.\overrightarrow{j},\ \overrightarrow{j}.\overrightarrow{k},\ \overrightarrow{k}.\overrightarrow{i\ }$ $\overrightarrow{i}^2,\ \overrightarrow{j}^2,\ \overrightarrow{k}^2,\ \overrightarrow{i}.\overrightarrow{j},\ \overrightarrow{j}.\overrightarrow{k},\ \overrightarrow{k}.\overrightarrow{i\ }$

c) Tính tích vô hướng $\overrightarrow{a}.\overrightarrow{b\ }$ $\overrightarrow{a}.\overrightarrow{b\ }$ theo toạ độ của hai vectơ $\overrightarrow{a\ }$ $\overrightarrow{a\ }$ và $\overrightarrow{b\ }$ $\overrightarrow{b\ }$.

Hướng dẫn giải:

a) Ta có:

$\vec{a}=a_1\vec{i}+a_2\vec{j}+a_3\vec{k\ }$ $\vec{a}=a_1\vec{i}+a_2\vec{j}+a_3\vec{k\ }$

$\vec{b}=b_1\vec{i}+b_2\vec{j}+b_3\vec{k\ }$ $\vec{b}=b_1\vec{i}+b_2\vec{j}+b_3\vec{k\ }$

b) $\overrightarrow{i}^2=\ \overrightarrow{j}^2=\ \overrightarrow{k}^2=1,\ \ \overrightarrow{i}.\overrightarrow{j}=\ \overrightarrow{j}.\overrightarrow{k}=\ \overrightarrow{k}.\overrightarrow{i\ }=0$ $\overrightarrow{i}^2=\ \overrightarrow{j}^2=\ \overrightarrow{k}^2=1,\ \ \overrightarrow{i}.\overrightarrow{j}=\ \overrightarrow{j}.\overrightarrow{k}=\ \overrightarrow{k}.\overrightarrow{i\ }=0$

c) $\overrightarrow{a}.\overrightarrow{b\ }=a_1b_1+a_2b_2+a_3b_3$ $\overrightarrow{a}.\overrightarrow{b\ }=a_1b_1+a_2b_2+a_3b_3$

-----------------------------------------------

---> Xem thêm: Giải Toán 12 trang 60 tập 1 Chân trời sáng tạo

Lời giải Toán 12 trang 59 Tập 1 Chân trời sáng tạo với các câu hỏi nằm trong Bài 3: Biểu thức toạ độ của các phép toán vectơ, được VnDoc biên soạn và đăng tải!

Chia sẻ, đánh giá bài viết

1

34

Bài trước

Bài sau