Giải Toán 8 trang 72 tập 2 Kết nối tri thức

Giải Toán 8 trang 72 Tập 2

Bài 8.10 trang 72 Toán 8 tập 2 Kết nối
Bài 8.11 trang 72 Toán 8 tập 2 Kết nối
Bài 8.12 trang 72 Toán 8 tập 2 Kết nối
Bài 8.13 trang 72 Toán 8 tập 2 Kết nối

Giải Toán 8 trang 72 Tập 2 Kết nối tri thức hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 8 Kết nối tri thức tập 2 trang 72.

Bài 8.10 trang 72 Toán 8 tập 2 Kết nối

Thống kê thời gian của 78 chương trình quảng cáo trên Đài truyền hình tỉnh X cho kết quả như sau:

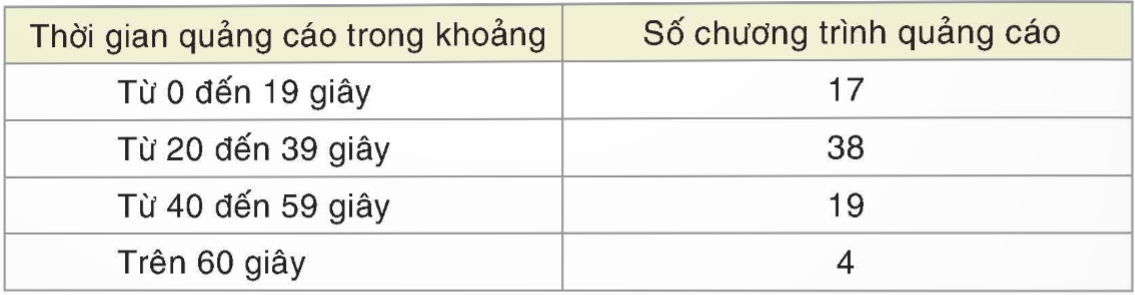
Tính xác suất thực nghiệm của các biến cố sau:

a) E: "Chương trình quảng cáo của Đài truyền hình tỉnh X kéo dài từ 20 đến 39 giây"

b) F: "Chương trình quảng cáo của Đài truyền hình tỉnh X kéo dài trên 1 phút"

c) G:" Chương trình quảng cáo của Đài truyền hình tỉnh X kéo dài trong khoảng từ 20 đến 59 giây"

Hướng dẫn giải:

a) Xác suất thực nghiệm của biến cố E: "Chương trình quảng cáo của Đài truyền hình tỉnh X kéo dài từ 20 đến 39 giây" là $\frac{38}{78}$ $\frac{38}{78}$

b) Xác suất thực nghiệm của biến cố F: "Chương trình quảng cáo của Đài truyền hình tỉnh X kéo dài trên 1 phút" là $\frac{4}{78}$ $\frac{4}{78}$

c) Số chương trình quảng cáo kéo dài từ 20 đến 59 giây là: 38 + 19

Vậy xác suất thực nghiệm của biến cố G là $\frac{38+19}{78} =\frac{57}{78}$ $\frac{38+19}{78} =\frac{57}{78}$.

Bài 8.11 trang 72 Toán 8 tập 2 Kết nối

Thống kê về số ca nhiễm bệnh và số ca tử vong của bệnh SARS và bệnh EBOLA được kết quả như sau:

Căn cứ vào bảng thống kê trên, hãy ước lượng xác suất một người tử vong khi nhiễm bệnh SARS, bệnh EBOLA.

Hướng dẫn giải:

Ước lượng xác suất một người tử vong khi nhiễm bệnh SARS là

$P(A)≈\frac{813}{8437}≈0,096=9,6\%$ $P(A)≈\frac{813}{8437}≈0,096=9,6\%$

Ước lượng xác suất một người tử vong khi nhiễm bệnh EBOLA là

$P\approx\frac{15158}{34453}\approx0,439\approx44\%$ $P\approx\frac{15158}{34453}\approx0,439\approx44\%$

Bài 8.12 trang 72 Toán 8 tập 2 Kết nối

Một nhà máy sản xuất máy điều hòa tiến hành kiểm tra chất lượng của 600 chiếc điều hòa được sản xuất và thấy có 5 chiếc bị lỗi. Trong một lô hàng có 1500 chiếc điều hòa, hãy dự đoán xem có khoảng bao nhiêu chiếc điều hòa không bị lỗi?

Hướng dẫn giải:

Số chiếc điều hòa không bị lỗi là: 600 – 5 = 595 chiếc

⇒ Xác suất để một chiếc điều hòa do nhà máy sản xuất không bị lỗi là: $\frac{595}{600}≈0,992$ $\frac{595}{600}≈0,992$

Gọi k là số lượng điều hòa không bị lỗi trong 1 500 chiếc điều hòa.

Ta có: $\frac{k}{1500}≈\frac{595}{600}$ $\frac{k}{1500}≈\frac{595}{600}$. Suy ra k = 1487,5

Vậy có khoảng 1 487 hoặc 1 488 chiếc điều hòa không bị lỗi trong 1500 chiếc.

Bài 8.13 trang 72 Toán 8 tập 2 Kết nối

Hai bạn Mai và Việt lần lượt thực hiện việc gieo đồng thời hai con xúc xắc và ở mỗi lần gieo sẽ nhận được số điểm bằng tổng số chấm xuất hiện trên hai con xúc xắc. Mai được gieo 100 lần và Việt được gieo 120 lần. Mai gieo trước và ghi lại kết quả của mình như sau: