Vở bài tập Toán lớp 5 bài 106 Luyện tập Diện tích xung quanh và diện tích toàn phần của hình chữ nhật
Vở bài tập Toán lớp 5 bài 106
Giải vở bài tập Toán 5 bài 106: Luyện tập Diện tích xung quanh và diện tích toàn phần của hình chữ nhật trang 24, 25, 26 Vở bài tập Toán 5 tập 2 có đáp án chi tiết giúp các em học sinh luyện tập cách giải các bài tập về diện tích xung quanh và diện tích toàn phần của hình hộp chữ nhật. Mời các em cùng tham khảo.
Bài tập Toán lớp 5 bài 106 là Hướng dẫn giải vở bài tập Toán lớp 5 tập 2 trang 24, 25, 26. Lời giải bao gồm 5 câu hỏi có đáp án chi tiết cho từng câu để các em học sinh so sánh đối chiếu với bài làm của mình. Các bậc Phụ huynh cùng tham khảo hướng dẫn con em học tập ôn luyện, củng cố tại nhà.
Vở bài tập toán lớp 5 tập 2 bài 106 Câu 1
Viết tiếp vào chỗ chấm cho thích hợp:
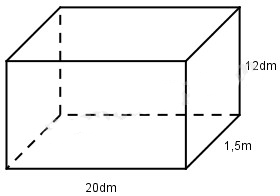
Một hình hộp chữ nhật có chiều dài 20dm, chiều rộng 1,5m và chiều cao 12dm.
a. Diện tích xung quanh của hình hộp chữ nhật là: ………………………..
b. Diện tích toàn phần của hình hộp chữ nhật là: …………………………
Phương pháp giải:
- Muốn tính diện tích xung quanh của hình hộp chữ nhật ta lấy chu vi mặt đáy nhân với chiều cao (cùng một đơn vị đo).
- Muốn tính diện tích toàn phần của hình hộp chữ nhật ta lấy diện tích xung quanh cộng với diện tích hai đáy.
Đáp án
Đổi:
20dm = 2m
12dm = 1,2m
Hướng dẫn
Chu vi mặt đáy hình hộp là:
(2 + 1,5) ⨯ 2 = 7 (m)
Diện tích xung quanh hình hộp là:
7 ⨯ 1,2 = 8,4 (m2)
Diện tích mặt đáy hình hộp là:
2 ⨯ 1,5 = 3 (m2)
Diện tích toàn phần hình hộp là:
8,4 + 2 ⨯ 3 = 14,4 (m2)
a. Diện tích xung quanh của hình hộp chữ nhật là 8,4m2
b. Diện tích toàn phần của hình hộp chữ nhật là 14,4m2
Vở bài tập toán lớp 5 tập 2 bài 106 Câu 2
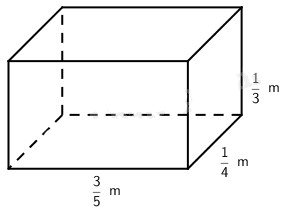
Tính diện tích xung quanh và diện tích toàn phần của hình hộp chữ nhật có chiều dài 3/5m, chiều rộng 1/4m và chiều cao 1/3m.
Phương pháp giải:
- Muốn tính diện tích xung quanh của hình hộp chữ nhật ta lấy chu vi mặt đáy nhân với chiều cao (cùng một đơn vị đo).
- Muốn tính diện tích toàn phần của hình hộp chữ nhật ta lấy diện tích xung quanh cộng với diện tích hai đáy.
Bài giải
Chu vi mặt đáy của hình hộp chữ nhật là:
\(\displaystyle \left( {{3 \over 5} + {1 \over 4}} \right) \times 2 = {{17} \over {10}}\left( m \right)\)
Diện tích xung quanh của hình hộp chữ nhật là:
\(\displaystyle {{17} \over {10}} \times {1 \over 3} = {{17} \over {30}}\,\left( {{m^2}} \right)\)
Diện tích mặt đáy của hình hộp chữ nhật là:
\(\displaystyle {3 \over 5} \times {1 \over 4} = {3 \over {20}}\,\left( {{m^2}} \right)\)
Diện tích toàn phần của hình hộp chữ nhật là:
\(\displaystyle {{17} \over {30}} + {3 \over {20}}\times 2 = {{13} \over {15}}\,\left( {{m^2}} \right)\)
Đáp số: Diện tích xung quanh: \(\displaystyle {{17} \over {30}}{m^2}\;\);
Diện tích toàn phần: \(\displaystyle {{13} \over {15}}{m^2}\).
Vở bài tập toán lớp 5 tập 2 bài 106 Câu 3
Khoanh vào chữ đặt trước câu trả lời đúng:
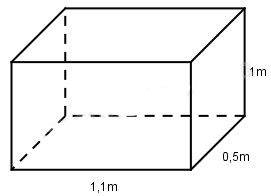
Diện tích xung quanh của hình hộp chữ nhật có chiều dài 1,1m, chiều rộng 0,5m và chiều cao 1m là:
A. 1,6m2
B. 3,2m2
C. 4,3m2
D. 3,75m2
Phương pháp giải:
- Tính chu vi mặt đáy = (chiều dài + chiều rộng) × 2.
- Diện tích xung quanh = chu vi mặt đáy × chiều cao.
Đáp án
Chọn đáp án B
Hướng dẫn
Chu vi mặt đáy hình hộp chữ nhật:
(1,1 + 0,5) ⨯ 2 = 3,2 (m)
Diện tích xung quanh hình hộp chữ nhật:
3,2 ⨯1 = 3,2 (m2)
Vở bài tập toán lớp 5 tập 2 bài 106 Câu 4
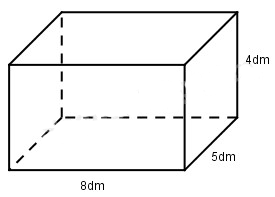
Người ta sơn toàn bộ mặt ngoài của một cái thùng tôn có nắp dạng hình hộp chữ nhật có chiều dài 8dm, chiều rộng 5dm và chiều cao 4dm. Hỏi diện tích được sơn bằng bao nhiêu đề-xi-mét-vuông?
Phương pháp giải:
- Diện tích sơn toàn bộ mặt ngoài của thùng tôn chính là diện tích 6 mặt của hình hộp chữ nhật cũng là diện tích toàn phần của hình hộp chữ nhật.
- Muốn tính diện tích toàn phần của hình hộp chữ nhật ta lấy diện tích xung quanh cộng với diện tích hai đáy.
Đáp án
Bài giải
Chu vi mặt đáy hình hộp chữ nhật là:
(8 + 5) ⨯ 2 = 26 (dm)
Diện tích xung quanh hình hộp là:
26 ⨯ 4 = 104 (dm2)
Diện tích mặt đáy hình hộp là:
8 ⨯ 5 = 40 (dm2)
Diện tích sơn là:
104 + 2 ⨯ 40 = 184 (dm2)
Đáp số: 184dm2
Vở bài tập toán lớp 5 tập 2 bài 106 Câu 5
Khoanh vào chữ đặt trước câu trả lời đúng:
Người ta xếp 4 hình lập phương bé có cạnh 1cm thành một hình hộp chữ nhật. Hỏi có bao nhiêu cách xếp khác nhau?
A. 1 cách
B. 2 cách
C. 3 cách
D. 4 cách
Phương pháp giải:
Dựa vào đặc điểm của hình chữ nhật để xếp 4 hình lập phương bé có cạnh 1cm thành một hình hộp chữ nhật.
Đáp án
Cách 1: Xếp 4 hình lập phương cạnh 1cm xếp chồng lên nhau ( chiều dài và chiều rộng đều là 1cm và chiều cao 4cm)
Cách 2: Xếp 4 hình lập phương cạnh 1cm xếp liền nhau theo hàng ngang (C hiều dài 4cm, chiều rộng và chiều cao đều là 1cm)
Vậy khoanh vào câu B.
>> Bài tiếp theo: Giải vở bài tập Toán 5 bài 107: Diện tích xung quanh và diện tích toàn phần của hình lập phương
Lý thuyết: Diện tích xung quanh và diện tích toàn phần của hình hộp chữ nhật
1. Diện tích xung quanh của hình hộp chữ nhật
- Diện tích xung quanh của hình hộp chữ nhật là tổng diện tích bốn mặt bên của hình hộp chữ nhật.
Quy tắc: Giử sử hình hộp chữ nhật có chiều dài là a, chiều rộng là b và chiều cao là h.
- Muốn tính diện tích xung quanh của hình hộp chữ nhật ta lấy chu vi mặt đáy nhân với chiều cao (cùng đơn vị đo).
Công thức tính: S = (a + b) × 2 × h
2. Diện tích toàn phần của hình hộp chữ nhật
- Diện tích toàn phần của hình hộp chữ nhật là tổng của diện tích xung quanh và diện tích hai đáy.
- Muốn tính diện tích toàn phần của hình hộp chữ nhật ta lấy diện tích xung quanh cộng với diện tích hai đáy.
Công thức tính: Stp = Sxq + Sđáy × 2 = (a + b) × 2 × h + 2 × a × b
Lưu ý:
- Chu vi mặt đáy bằng tổng của chiều dài và chiều rộng nhân với 22.
- Diện tích mặt đáy bằng tích của chiều dài và chiều rộng.
>> Tham khảo: Lý thuyết Diện tích xung quanh và diện tích toàn phần của hình hộp chữ nhật
.....................
Ngoài ra, các em học sinh lớp 5 còn có thể tham khảo Giải bài tập SGK Toán 5: Diện tích xung quanh và diện tích toàn phần hình hộp chữ nhật hay đề thi học kì 2 lớp 5 đầy đủ các môn học Toán, Tiếng Việt, Tiếng Anh, Khoa học, Lịch sử - Địa lý, Tin học mà VnDoc.com đã sưu tầm và chọn lọc. Hy vọng với những tài liệu này, các em học sinh sẽ học tốt môn Toán lớp 5 hơn mà không cần sách giải.
