VnDoc.com

Giải Toán 12 trang 81 tập 1 Cánh diều

Bài trước

Tải về

Bài sau

Giải Toán 12 trang 81 Cánh diều Tập 1

Bài 5 trang 81 SGK Toán 12 tập 1
Bài 6 trang 81 SGK Toán 12 tập 1
Bài 7 trang 81 SGK Toán 12 tập 1
Bài 8 trang 81 SGK Toán 12 tập 1

Giải Toán 12 trang 81 Tập 1 hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 12 Cánh diều tập 1 trang 81.

Bài 5 trang 81 SGK Toán 12 tập 1

Trong không gian với hệ tọa độ Oxyz, cho $\overrightarrow{a\ }$ $\vec{a}$ = (3; 2; − 1), $\overrightarrow {b }$ $\vec{b}$ = (− 2; 1; 2). Tính côsin của góc ( $\overrightarrow{a\ }$ $\vec{a}$ , $\overrightarrow {b }$ $\vec{b}$ ).

Hướng dẫn giải:

Ta có: $\cos (\overrightarrow{a},\overrightarrow{b})=\frac{-6+2-2}{\sqrt{14} .3} =-\frac{2}{\sqrt{14} }$ $\cos (\vec{a}, \vec{b}) = \frac{- 6 + 2 - 2}{\sqrt{14} .3} = - \frac{2}{\sqrt{14}}$

Bài 6 trang 81 SGK Toán 12 tập 1

Trong không gian với hệ tọa độ Oxyz, cho A(– 2; 3; 0), B(4; 0; 5), C(0; 2; – 3).

a) Chứng minh rằng ba điểm A, B, C không thẳng hàng.

b) Tính chu vi tam giác ABC.

c) Tìm tọa độ trọng tâm G của tam giác ABC.

d) Tính $\cos \widehat {BAC}$ $\cos \hat{B A C}$ .

Hướng dẫn giải:

a) Ta có: $\overrightarrow{AB}=\left(6;-3;5\right)$ $\vec{A B} = (6; - 3; 5)$ , $\overrightarrow{AC}=\left(2;-1;-3\right)$ $\vec{A C} = (2; - 1; - 3)$

Suy ra $\overrightarrow{AB}\ne k\overrightarrow{AC}$ $\vec{A B} \neq k \vec{A C}$ với mọi k thuộc R

Vậy A, B, C không thẳng hàng.

b) $\overrightarrow{BC}=\left(-4;2;-8\right)$ $\vec{B C} = (- 4; 2; - 8)$

Ta có: AB = $\sqrt{70}$ $\sqrt{70}$ ; AC = $\sqrt{14}$ $\sqrt{14}$ ; BC = $2\sqrt{21}$ $2 \sqrt{21}$

Vậy chu vi tam giác ABC là: $\sqrt{70}+\sqrt{14}+2\sqrt{21}$ $\sqrt{70} + \sqrt{14} + 2 \sqrt{21}$

c) Do G là trọng tâm của tam giác ABC nên $G\left(\frac{2}{3};\frac{5}{3};\frac{2}{3}\right)$ $G (\frac{2}{3}; \frac{5}{3}; \frac{2}{3})$

d) $\cos\widehat{BAC}=\frac{\overrightarrow{AB}.\overrightarrow{AC}}{|\overrightarrow{AB}|.|\overrightarrow{AC}|}=\frac{12+3-15}{\sqrt{70}. \sqrt{14}}=0$ $\cos \hat{B A C} = \frac{\vec{A B} . \vec{A C}}{| \vec{A B} | . | \vec{A C} |} = \frac{12 + 3 - 15}{\sqrt{70} . \sqrt{14}} = 0$

Bài 7 trang 81 SGK Toán 12 tập 1

Cho hình hộp ABCD.A'B'C'D', biết A(1; 0; 1), B(2; 1; 2), D(1; – 1; 1), C'(4; 5; – 5). Hãy chỉ ra tọa độ của một vectơ khác $\overrightarrow{0\ }$ $\vec{0}$ vuông góc với cả hai vectơ trong mỗi trường hợp sau:

a) $\overrightarrow{AC}$ $\vec{A C}$ và $\overrightarrow{B$ $\vec{B^{'} D^{'}}$

b) $\overrightarrow{AC$ $\vec{A C^{'}}$ và $\overrightarrow{BD}$ $\vec{B D}$ .

Hướng dẫn giải:

Đang cập nhật...

Bài 8 trang 81 SGK Toán 12 tập 1

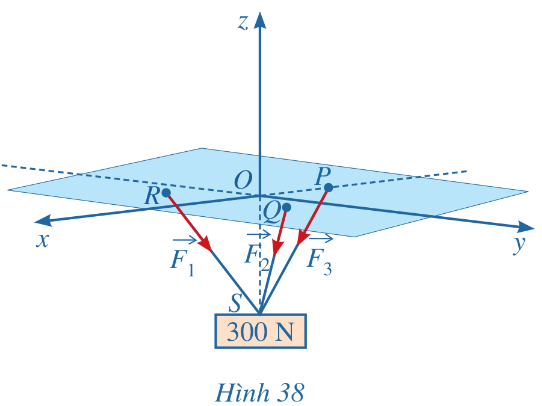
Một vật có trọng lượng 300 N được treo bằng ba sợi dây cáp không dãn có chiều dài bằng nhau, mỗi dây cáp có một đầu được gắn tại một trong các điểm P(– 2; 0; 0), Q(1; $\sqrt{3}$ $\sqrt{3}$ ; 0), R(1; $-\sqrt{3}$ $- \sqrt{3}$ ; 0) còn đầu kia gắn với vật tại điểm S(0; 0; $-2\sqrt{3}$ $- 2 \sqrt{3}$ ) như Hình 38. Gọi $\overrightarrow{F_1},\overrightarrow{F_2},\overrightarrow{F_3}$ $\vec{F_{1}}, \vec{F_{2}}, \vec{F_{3}}$ lần lượt là lực căng trên các sợi dây cáp RS, QS và PS. Tìm tọa độ của các lực $\overrightarrow{F_1},\overrightarrow{F_2},\overrightarrow{F_3}$ $\vec{F_{1}}, \vec{F_{2}}, \vec{F_{3}}$ .

Hướng dẫn giải:

Đang cập nhật...

-----------------------------------------------

---> Xem thêm: Giải Toán 12 trang 82 tập 1 Cánh diều

Lời giải Toán 12 trang 81 Tập 1 Cánh diều với các câu hỏi nằm trong Toán 12 Cánh diều Bài 3: Biểu thức toạ độ của các phép toán vectơ, được VnDoc biên soạn và đăng tải!

Chia sẻ, đánh giá bài viết

1

42

Bài trước

Bài sau

Chia sẻ bởi:
Lê Jelar

Đóng Chỉ thành viên VnDoc PRO/PROPLUS tải được nội dung này!

Đóng

79.000 / tháng

Mua ngay

Đặc quyền các gói Thành viên

PRO

Phổ biến nhất

PRO+

Tải tài liệu Cao cấp 1 Lớp

Tải tài liệu Trả phí + Miễn phí

Xem nội dung bài viết

Trải nghiệm Không quảng cáo

Làm bài trắc nghiệm không giới hạn

Tìm hiểu thêm

Mua cả năm Tiết kiệm tới 48%

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!