Giải Toán 12 trang 71 tập 1 Cánh diều
Giải Toán 12 trang 71 Cánh diều Tập 1
Giải Toán 12 trang 71 Tập 1 hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 12 Cánh diều tập 1 trang 71.
Hoạt động 6 trang 71 SGK Toán 12 tập 1
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(xA; yA; zA), B(xB; yB; zB) (Hình 32).
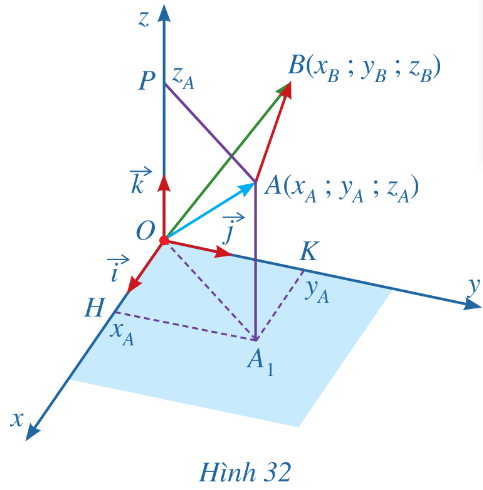
a) Biểu diễn mỗi vectơ 
\(\overrightarrow{OA},\ \overrightarrow{OB}\) theo các vectơ \(\overrightarrow{i},\ \overrightarrow{j\ }\) và \(\overrightarrow{k\ }\)
b) Tìm liên hệ giữa \(\overrightarrow{AB}\) và \(\left(x_B-x_A\right)\overrightarrow{i}+\left(y_B-y_A\right)\overrightarrow{j}+\left(z_B-z_A\right)\overrightarrow{k}\)
c) Từ đó, tìm tọa độ của vectơ \(\overrightarrow{AB}\).
Hướng dẫn giải:
a) Ta có: \(\overrightarrow{OA}=x_A\ \overrightarrow{i\ }+y_A\ \overrightarrow{j\ }+z_A\ \overrightarrow{k\ }\)
\(\overrightarrow{OB}=x_B\ \overrightarrow{i\ }+y_B\ \overrightarrow{j\ }+z_B\ \overrightarrow{k\ }\)
b) \(\overrightarrow{AB\ }=\left(x_B-x_A\right)\overrightarrow{i}+\left(y_B-y_A\right)\overrightarrow{j}+\left(z_B-z_A\right)\overrightarrow{k\ }\)
c) Từ câu b, ta có:
\(\overrightarrow{AB}\) = (xB – xA; yB – yA; zB – zA)
Luyện tập 6 trang 71 SGK Toán 12 tập 1
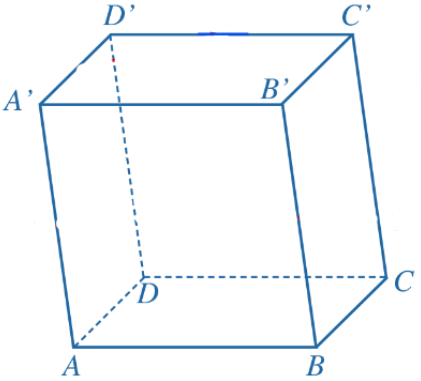
Trong không gian với hệ tọa độ Oxyz, cho hình hộp ABCD.A'B'C'D' có A'(1; 0; 1), B'(2; 1; 2), D'(1; – 1; 1), C(4; 5; – 5). Tìm tọa độ đỉnh A của hình hộp ABCD.A'B'C'D'.
Hướng dẫn giải:
Ta có: \(\overrightarrow{A'B'}\) = (1; 1; 1)
Giả sử tọa độ điểm D là D(x; y; z) nên \(\overrightarrow{DC}\) = (4 – x; 5 – y; – 5 – z)
Do ABCD.A'B'C'D' là hình hộp nên \(\overrightarrow{A'B'}\) = \(\overrightarrow{DC}\)
Suy ra 4 – x = 1; 5 – y = 1; – 5 – z = 1 hay x = 3; y = 4; z = – 6
Vậy D(3; 4; – 6)
Giả sử tọa độ điểm A là A(a; b; c)
Ta có: \(\overrightarrow{A'A}=\left(a-1;b;c-1\right);\ \overrightarrow{D'D}=\left(2;5;-7\right)\)
Do ABCD.A'B'C'D' là hình hộp nên \(\overrightarrow{A'A}=\ \overrightarrow{D'D}\)
Suy ra a – 1 = 2; b = 5; c – 1 = – 7 hay a = 3; b = 5; c = – 6
Vậy A(3; 5; – 6).
-----------------------------------------------
---> Xem thêm: Giải Toán 12 trang 72 tập 1 Cánh diều
Lời giải Toán 12 trang 71 Tập 1 Cánh diều với các câu hỏi nằm trong Toán 12 Cánh diều Bài 2: Toạ độ của vectơ, được VnDoc biên soạn và đăng tải!
