Giải Toán 12 trang 60 tập 1 Cánh diều

Giải Toán 12 trang 60 Cánh diều Tập 1

Hoạt động 5 trang 60 SGK Toán 12 tập 1
Luyện tập 5 trang 60 SGK Toán 12 tập 1

Giải Toán 12 trang 60 Tập 1 hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 12 Cánh diều tập 1 trang 60.

Hoạt động 5 trang 60 SGK Toán 12 tập 1

Nêu định nghĩa tích của một số thực k ≠ 0 với vecto $\vec{a}\ne\vec{0}$ $\vec{a} \neq \vec{0}$ trong mặt phẳng

Hướng dẫn giải:

Cho số thực k ≠ 0 với vecto $\vec{a}\ne\vec{0}$ $\vec{a} \neq \vec{0}$ . Tích của số k với vectơ $\vec{a}$ $\vec{a}$ là một vectơ, kí hiệu là $k\vec{a}$ $k \vec{a}$ .

Luyện tập 5 trang 60 SGK Toán 12 tập 1

Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AD và BC, I là trung điểm MN. Chứng minh rằng:

a) $\overrightarrow{MN}=\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{DC})$ $\vec{M N} = \frac{1}{2} (\vec{A B} + \vec{D C})$

b) $\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}=\overrightarrow{0\ }$ $\vec{I A} + \vec{I B} + \vec{I C} + \vec{I D} = \vec{0}$

Hướng dẫn giải:

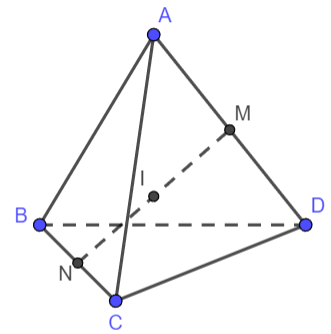
a) Ta có:

$\overrightarrow{MN}=\overrightarrow{MA}+\overrightarrow{AN}=\frac{1}{2}\overrightarrow{DA}+\frac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AC}\right)$ $\vec{M N} = \vec{M A} + \vec{A N} = \frac{1}{2} \vec{D A} + \frac{1}{2} (\vec{A B} + \vec{A C})$

$=\frac{1}{2}\overrightarrow{AB}+\frac{1}{2}\left(\overrightarrow{DA}+\overrightarrow{AC}\right)$ $= \frac{1}{2} \vec{A B} + \frac{1}{2} (\vec{D A} + \vec{A C})$

$=\frac{1}{2}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{DC}$ $= \frac{1}{2} \vec{A B} + \frac{1}{2} \vec{D C}$

b) Ta có: $\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}$ $\vec{I A} + \vec{I B} + \vec{I C} + \vec{I D}$

$= (\overrightarrow{IA}+\overrightarrow{ID} )+ (\overrightarrow{IB}+\overrightarrow{IC} )$ $= (\vec{I A} + \vec{I D}) + (\vec{I B} + \vec{I C})$

$=2\overrightarrow{IM}+2\overrightarrow{IN}$ $= 2 \vec{I M} + 2 \vec{I N}$

$=2(\overrightarrow{IM}+\overrightarrow{IN})=\overrightarrow{0\ }$ $= 2 (\vec{I M} + \vec{I N}) = \vec{0}$

-----------------------------------------------

---> Xem thêm: Giải Toán 12 trang 61 tập 1 Cánh diều

Lời giải Toán 12 trang 60 Tập 1 Cánh diều với các câu hỏi nằm trong Toán 12 Cánh diều Bài 1: Vectơ và các phép toán vectơ trong không gian, được VnDoc biên soạn và đăng tải!

Chia sẻ, đánh giá bài viết

1

42

Bài trước

Bài sau

Chia sẻ bởi:
Lê Jelar

Đóng Chỉ thành viên VnDoc PRO/PROPLUS tải được nội dung này!

Đóng

79.000 / tháng

Mua ngay

Đặc quyền các gói Thành viên

PRO

Phổ biến nhất

PRO+

Tải tài liệu Cao cấp 1 Lớp

Tải tài liệu Trả phí + Miễn phí

Xem nội dung bài viết

Trải nghiệm Không quảng cáo

Làm bài trắc nghiệm không giới hạn

Tìm hiểu thêm

Mua cả năm Tiết kiệm tới 48%

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!