Giải Toán 12 trang 61 tập 1 Cánh diều
Giải Toán 12 trang 61 Cánh diều Tập 1
Giải Toán 12 trang 61 Tập 1 hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 12 Cánh diều tập 1 trang 61.
Hoạt động 6 trang 61 SGK Toán 12 tập 1
Trong không gian, cho hai vectơ 
\(\vec{a},\vec{b}\) khác \(\vec{0}\). Lấy một điểm O tùy ý.
a) Vẽ hai vectơ \(\overrightarrow{OA}=\vec{a},\overrightarrow{OB}=\vec{b}\)
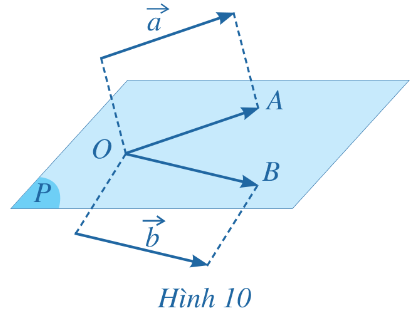
b) Khi đó, hai vectơ \(\overrightarrow{OA},\overrightarrow{OB}\) có giá cùng nằm trong mặt phẳng (P) (Hình 10). Nêu định nghĩa góc giữa hai vectơ \(\overrightarrow{OA},\overrightarrow{OB}\) trong mặt phẳng (P)
Hướng dẫn giải:
Luyện tập 6 trang 61 SGK Toán 12 tập 1
Cho tứ diện đều ABCD. Gọi M, N lần lượt là trung điểm các cạnh AB, AC. Hãy tính góc giữa hai vectơ \(\overrightarrow{MN},\overrightarrow{BD}\).
Hướng dẫn giải:
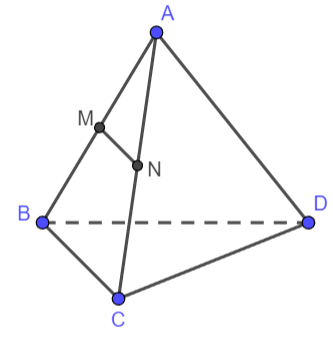
Ta có: M, N là trung điểm của AB và AC nên MN là đường trung bình của tam giác ABC
=> MN // BC
Do đó \((\overrightarrow{MN},\overrightarrow{BD})=(\overrightarrow{BC},\overrightarrow{BD})= \widehat{CBD}\)
Vì ABCD là tứ diện đều nên tam giác BCD đều.
Vậy \(\widehat{CBD}=60^{\circ}\) hay (\(\overrightarrow{MN},\overrightarrow{BD}\)) = 60o.
Hoạt động 7 trang 61 SGK Toán 12 tập 1
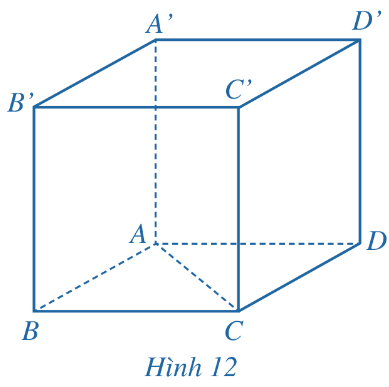
Trong không gian, cho hình lập phương ABCD.A'B'C'D' có độ dài bằng 3 cm (Hình 12).
a) Tính góc giữa hai vectơ \(\overrightarrow{AC},\overrightarrow{A'D'}\)
b) Tính \(|\overrightarrow{AC}|.|\overrightarrow{A'D'}|.\cos(\overrightarrow{AC},\overrightarrow{A'D'})\)
Hướng dẫn giải:
a) Ta có: \(\overrightarrow{A'D'}=\overrightarrow{AD}\)
Do đó \((\overrightarrow{AC},\overrightarrow{A'D'})=(\overrightarrow{AC},\overrightarrow{AD})= \widehat{CAD}\) = 45o.
b) \(|\overrightarrow{AC}|.|\overrightarrow{A'D'}|.\cos(\overrightarrow{AC},\overrightarrow{A'D'})\)
\(=3\sqrt{2}.3.\cos60^{\circ} =\frac{9\sqrt{2}}{2}\)
-----------------------------------------------
---> Xem thêm: Giải Toán 12 trang 62 tập 1 Cánh diều
Lời giải Toán 12 trang 61 Tập 1 Cánh diều với các câu hỏi nằm trong Toán 12 Cánh diều Bài 1: Vectơ và các phép toán vectơ trong không gian, được VnDoc biên soạn và đăng tải!
