Giải Toán 12 trang 59 tập 1 Cánh diều
Giải Toán 12 trang 59 Cánh diều Tập 1
Giải Toán 12 trang 59 Tập 1 hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 12 Cánh diều tập 1 trang 59.
Hoạt động 3 trang 59 SGK Toán 12 tập 1
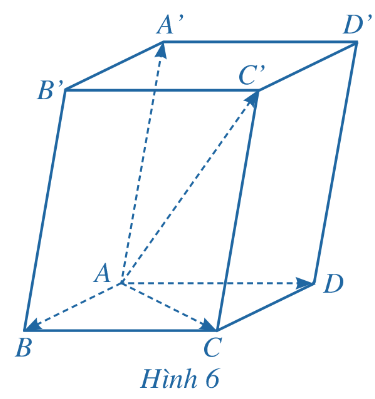
Cho hình hộp ABCD . A'B'C'D'. Tìm liên hệ giữa 
\(\overrightarrow{AB}+\overrightarrow{AD}\) và \(\overrightarrow{AC};\ \overrightarrow{AC}+\overrightarrow{AA'}\) và \(\overrightarrow{AC'}\)
Từ đó, hãy suy ra rằng \(\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{AA'}=\overrightarrow{AC'}\)
Hướng dẫn giải:
Ta có: ABCD là hình bình hành nên \(\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}\) (quy tắc hình bình hành)
AA'C'A là hình bình hành nên \(\overrightarrow{AA'}+\overrightarrow{AC}=\overrightarrow{AC'}\) (quy tắc hình bình hành)
Do đó \(\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{AA'}=\overrightarrow{AC}+\overrightarrow{AA'}=\overrightarrow{AC'}\)
Luyện tập 3 trang 59 SGK Toán 12 tập 1
Cho hình hộp ABCD . A'B'C'D'. Chứng minh rằng: \(\overrightarrow{B'B}+\overrightarrow{AD}+\overrightarrow{CD}=\overrightarrow{B'D}\)
Hướng dẫn giải:
Ta có: \(\overrightarrow{AD}=\overrightarrow{B'C'};\ \overrightarrow{CD}=\ \overrightarrow{B'A'}\)
Do đó: \(\overrightarrow{B'B}+\overrightarrow{AD}+\overrightarrow{CD}=\overrightarrow{B'B}+\overrightarrow{B'C'}+\overrightarrow{B'A'}=\overrightarrow{B'D}\)
Hoạt động 4 trang 59 SGK Toán 12 tập 1
Trong không gian , cho hai vectơ \(\vec{a},\vec{b}\). Lấy một điểm M tùy ý
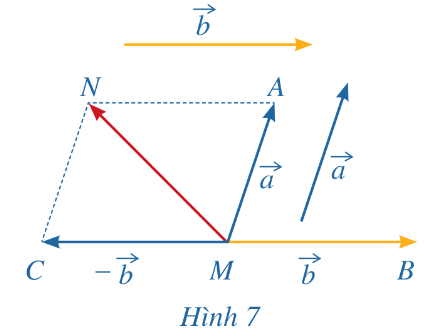
a) Vẽ \(\overrightarrow{MA}=\vec{a},\overrightarrow{MB}=\vec{b},\overrightarrow{MC}=-\overrightarrow{b\ }\)
b) Tổng của hai vectơ \(\vec{a}\) và \(-\vec{b}\) bằng vectơ nào trong hình 7?
Hướng dẫn giải:
a) Vẽ hình.
b) Tổng của hai vectơ \(\vec{a}\) và \(-\vec{b}\) bằng vectơ \(\overrightarrow{MN}\)
Luyện tập 4 trang 59 SGK Toán 12 tập 1
Cho hình hộp ABCD . A'B'C'D'. Chứng minh rằng: \(\overrightarrow{BB'}-\overrightarrow{C'B'}-\overrightarrow{D'C'}=\overrightarrow{BD'}\)
Hướng dẫn giải:
Ta có:
\(\overrightarrow{BB'}-\overrightarrow{C'B'}-\overrightarrow{D'C'}=\overrightarrow{BB'}+(-\overrightarrow{C'B'})+(-\overrightarrow{D'C'})\)
\(=\overrightarrow{BB'}+\overrightarrow{B'C'}+\overrightarrow{C'D'}\)
\(=\overrightarrow{BC'}+\overrightarrow{C'D'}=\overrightarrow{BD'}\)
-----------------------------------------------
---> Xem thêm: Giải Toán 12 trang 60 tập 1 Cánh diều
Lời giải Toán 12 trang 59 Tập 1 Cánh diều với các câu hỏi nằm trong Toán 12 Cánh diều Bài 1: Vectơ và các phép toán vectơ trong không gian, được VnDoc biên soạn và đăng tải!
