Giải Toán 12 trang 74 tập 1 Cánh diều

Giải Toán 12 trang 74 Cánh diều Tập 1

Hoạt động 1 trang 74 SGK Toán 12 tập 1

Giải Toán 12 trang 74 Tập 1 hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 12 Cánh diều tập 1 trang 74.

Hoạt động 1 trang 74 SGK Toán 12 tập 1

Trong không gian với hệ tọa độ Oxyz (Hình 36), cho hai vectơ $\overrightarrow{u}=(x_1;y_1;z_1)$ $\overrightarrow{u}=(x_1;y_1;z_1)$ và $\overrightarrow{v}=(x_2;y_2;z_2)$ $\overrightarrow{v}=(x_2;y_2;z_2)$

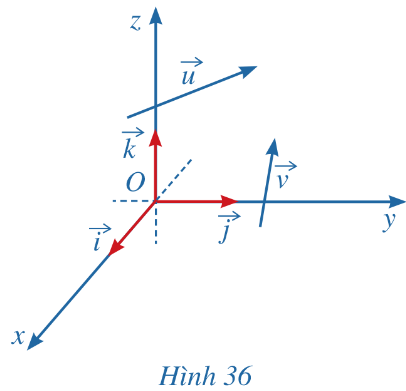
a) Biểu diễn các vectơ $\overrightarrow{u},\ \overrightarrow{v\ }$ $\overrightarrow{u},\ \overrightarrow{v\ }$ theo ba vectơ $\overrightarrow{i},\ \overrightarrow{j},\overrightarrow{k\ }$ $\overrightarrow{i},\ \overrightarrow{j},\overrightarrow{k\ }$

b) Biểu diễn các vectơ $\overrightarrow{u}+\overrightarrow{v},\ \overrightarrow{u}-\overrightarrow{v},\ m\overrightarrow{u}\ \left(m\in R\right)$ $\overrightarrow{u}+\overrightarrow{v},\ \overrightarrow{u}-\overrightarrow{v},\ m\overrightarrow{u}\ \left(m\in R\right)$ theo ba vectơ $\overrightarrow{i},\overrightarrow{j},\overrightarrow{k\ }$ $\overrightarrow{i},\overrightarrow{j},\overrightarrow{k\ }$

c) Tìm tọa độ các vectơ $\overrightarrow{u}+\overrightarrow{v},\ \overrightarrow{u}-\overrightarrow{v},\ m\overrightarrow{u}\ \left(m\in R\right)$ $\overrightarrow{u}+\overrightarrow{v},\ \overrightarrow{u}-\overrightarrow{v},\ m\overrightarrow{u}\ \left(m\in R\right)$

Hướng dẫn giải:

a) Ta có:

$\overrightarrow{u}=(x_1;y_1;z_1)$ $\overrightarrow{u}=(x_1;y_1;z_1)$ nên $\overrightarrow{u}=x_1\overrightarrow{i}+y_1\overrightarrow{j}+z_1\overrightarrow{k\ }$ $\overrightarrow{u}=x_1\overrightarrow{i}+y_1\overrightarrow{j}+z_1\overrightarrow{k\ }$

$\overrightarrow{v}=(x_2;y_2;z_2)$ $\overrightarrow{v}=(x_2;y_2;z_2)$ nên $\overrightarrow{v}=x_2\overrightarrow{i}+y_2\overrightarrow{j}+z_2\overrightarrow{k\ }$ $\overrightarrow{v}=x_2\overrightarrow{i}+y_2\overrightarrow{j}+z_2\overrightarrow{k\ }$

b) $\overrightarrow{u}+\overrightarrow{v}=\left(x_1+x_2\right)\overrightarrow{i}+\left(y_1+y_2\right)\overrightarrow{j}+\left(z_1+z_2\right)\overrightarrow{k\ }$ $\overrightarrow{u}+\overrightarrow{v}=\left(x_1+x_2\right)\overrightarrow{i}+\left(y_1+y_2\right)\overrightarrow{j}+\left(z_1+z_2\right)\overrightarrow{k\ }$

$\overrightarrow{u}-\overrightarrow{v}=\left(x_1-x_2\right)\overrightarrow{i}+\left(y_1-y_2\right)\overrightarrow{j}+\left(z_1-z_2\right)\overrightarrow{k}$ $\overrightarrow{u}-\overrightarrow{v}=\left(x_1-x_2\right)\overrightarrow{i}+\left(y_1-y_2\right)\overrightarrow{j}+\left(z_1-z_2\right)\overrightarrow{k}$

$m\overrightarrow{u}=mx_1\overrightarrow{i}+my_1\overrightarrow{j}+mz_1\overrightarrow{k\ }$ $m\overrightarrow{u}=mx_1\overrightarrow{i}+my_1\overrightarrow{j}+mz_1\overrightarrow{k\ }$

c) Từ câu b, ta có:

$\overrightarrow{u}+\overrightarrow{v}=\left(x_1+x_2;y_1+y_2;z_1+z_2\right)$ $\overrightarrow{u}+\overrightarrow{v}=\left(x_1+x_2;y_1+y_2;z_1+z_2\right)$

$\overrightarrow{u}-\overrightarrow{v}=\left(x_1-x_2;y_1-y_2;z_1-z_2\right)$ $\overrightarrow{u}-\overrightarrow{v}=\left(x_1-x_2;y_1-y_2;z_1-z_2\right)$

$m\overrightarrow{u}=\left(mx_1;my_1;mz_1\right)$ $m\overrightarrow{u}=\left(mx_1;my_1;mz_1\right)$

-----------------------------------------------

---> Xem thêm: Giải Toán 12 trang 75 tập 1 Cánh diều

Lời giải Toán 12 trang 74 Tập 1 Cánh diều với các câu hỏi nằm trong Toán 12 Cánh diều Bài 3: Biểu thức toạ độ của các phép toán vectơ, được VnDoc biên soạn và đăng tải!

Chia sẻ, đánh giá bài viết

1

9

Bài trước

Bài sau