Giải Toán 12 trang 57 tập 1 Cánh diều
Giải Toán 12 trang 57 Cánh diều Tập 1
Giải Toán 12 trang 57 Tập 1 hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 12 Cánh diều tập 1 trang 57.
Luyện tập 1 trang 57 SGK Toán 12 tập 1
Cho hình hộp ABCD . A'B'C'D'. Hãy chỉ ra ba vectơ có điểm đầu và điểm cuối là các đỉnh của hình hộp sao cho mỗi vectơ đó:
a) Bằng vectơ 
\(\overrightarrow{AA'}\)
b) Là vectơ đối của vectơ \(\overrightarrow{AA'}\)
Hướng dẫn giải:
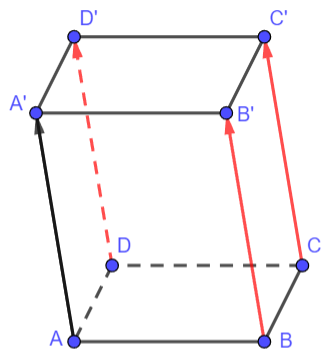
a) Do các vectơ \(\overrightarrow{BB'},\ \overrightarrow{CC'},\ \overrightarrow{DD'}\) cùng hướng với \(\overrightarrow{AA'}\) và AA' = BB' = CC' = DD' (tính chất hình hộp) nên \(\overrightarrow{AA'}=\overrightarrow{BB'}=\overrightarrow{CC'}=\overrightarrow{DD'}\)
Vậy ba vectơ \(\overrightarrow{BB'},\ \overrightarrow{CC'},\ \overrightarrow{DD'}\) có điểm đầu và điểm cuối là các đỉnh của hình hộp và bằng vectơ \(\overrightarrow{AA'}\)
a) Do các vectơ \(\overrightarrow{B'B},\ \overrightarrow{C'C},\ \overrightarrow{D'D}\) ngược hướng với \(\overrightarrow{AA'}\) và AA' = B'B = C'C = D'D (tính chất hình hộp) nên ba vectơ \(\overrightarrow{B'B},\ \overrightarrow{C'C},\ \overrightarrow{D'D}\) là ba vectơ đối của vectơ \(\overrightarrow{AA'}\).
-----------------------------------------------
---> Xem thêm: Giải Toán 12 trang 58 tập 1 Cánh diều
Lời giải Toán 12 trang 57 Tập 1 Cánh diều với các câu hỏi nằm trong Toán 12 Cánh diều Bài 1: Vectơ và các phép toán vectơ trong không gian, được VnDoc biên soạn và đăng tải!
